XY-Chain

Prerequisite: Chain basics

---

1. Overview

XY-Chain is a chain technique built only from bivalue cells (cells with exactly 2 candidates).

Compared to X-Chain:

• X-Chain focuses on one digit d (nodes are candidates of d)
• XY-Chain focuses on bivalue cells, so the chain can switch between different digits

The core idea in plain words:

In a bivalue cell, it’s always “either X or Y”.
Combine that with “same digit in the same house can’t both be true”, and the reasoning can propagate.

When the two endpoints happen to be the same digit (for example both are candidate 2), any candidate 2 that can see both endpoints can be eliminated.

---

2. Walkthrough

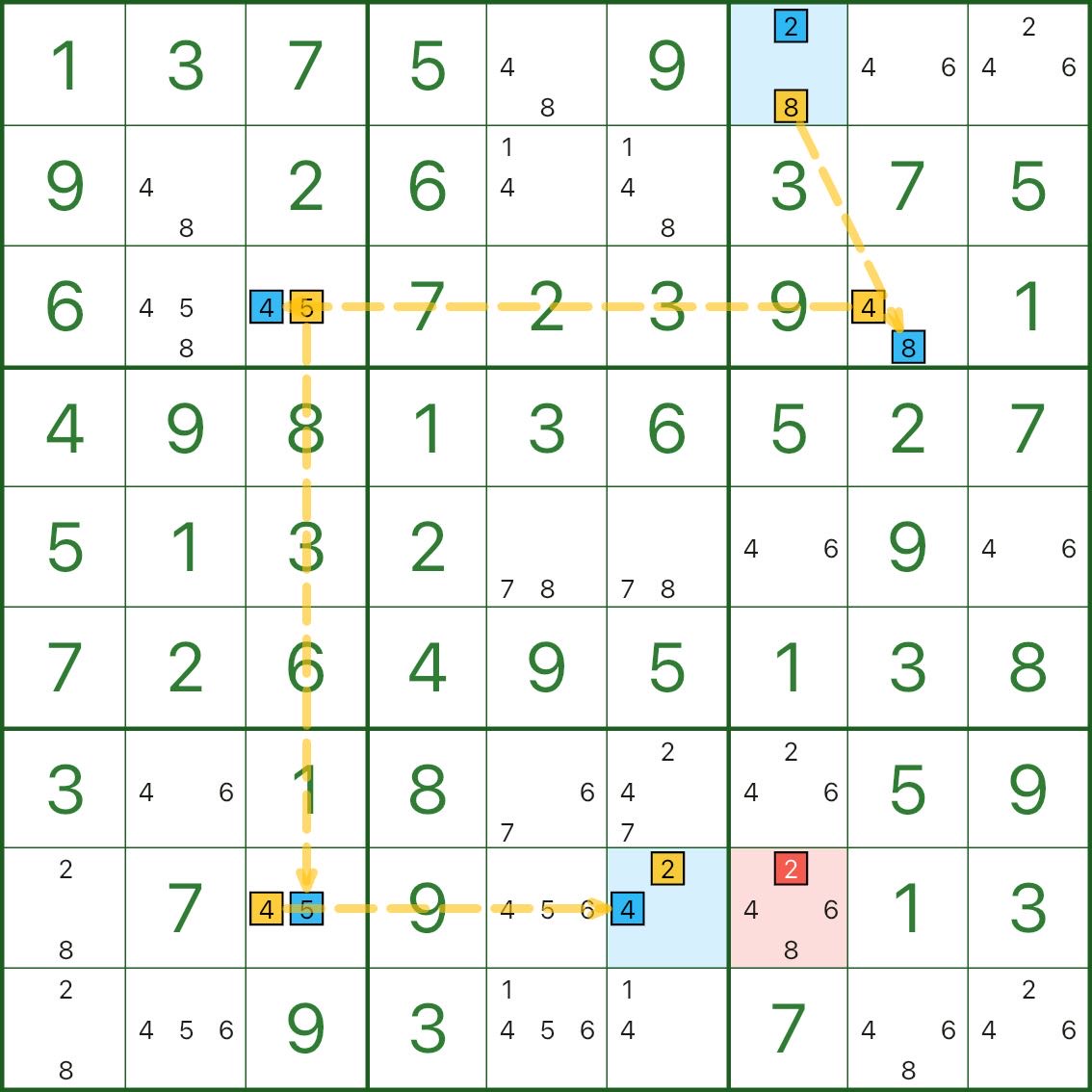
In the image, the blue cells are the chain endpoints, and the target digit is 2:

• Start: candidate 2 in r1c7
• End: candidate 2 in r8c6
• Elimination: candidate 2 in r8c7 (red)

Why can we eliminate 2 in r8c7? A short contradiction is enough:

1. Assume the red candidate r8c7 = 2 is true
2. Since r8c7 can see both endpoints:
   • same column ⇒ r1c7 cannot be 2
   • same row ⇒ r8c6 cannot be 2
3. But the chain connects r1c7#2 to r8c6#2. In a bivalue-only chain, making one end false propagates and eventually forces the other end true
   ⇒ r1c7 is not 2 forces r8c6 must be 2
4. This contradicts step 2 (“r8c6 cannot be 2”)

So the assumption is impossible: candidate 2 in r8c7 can be eliminated.

---

3. Examples

Here are two more XY-Chain examples. You don’t need to verify every step at first — focus on the three key pieces:

• the two blue endpoints
• a path made of bivalue cells
• a red elimination that typically sees both endpoints

---

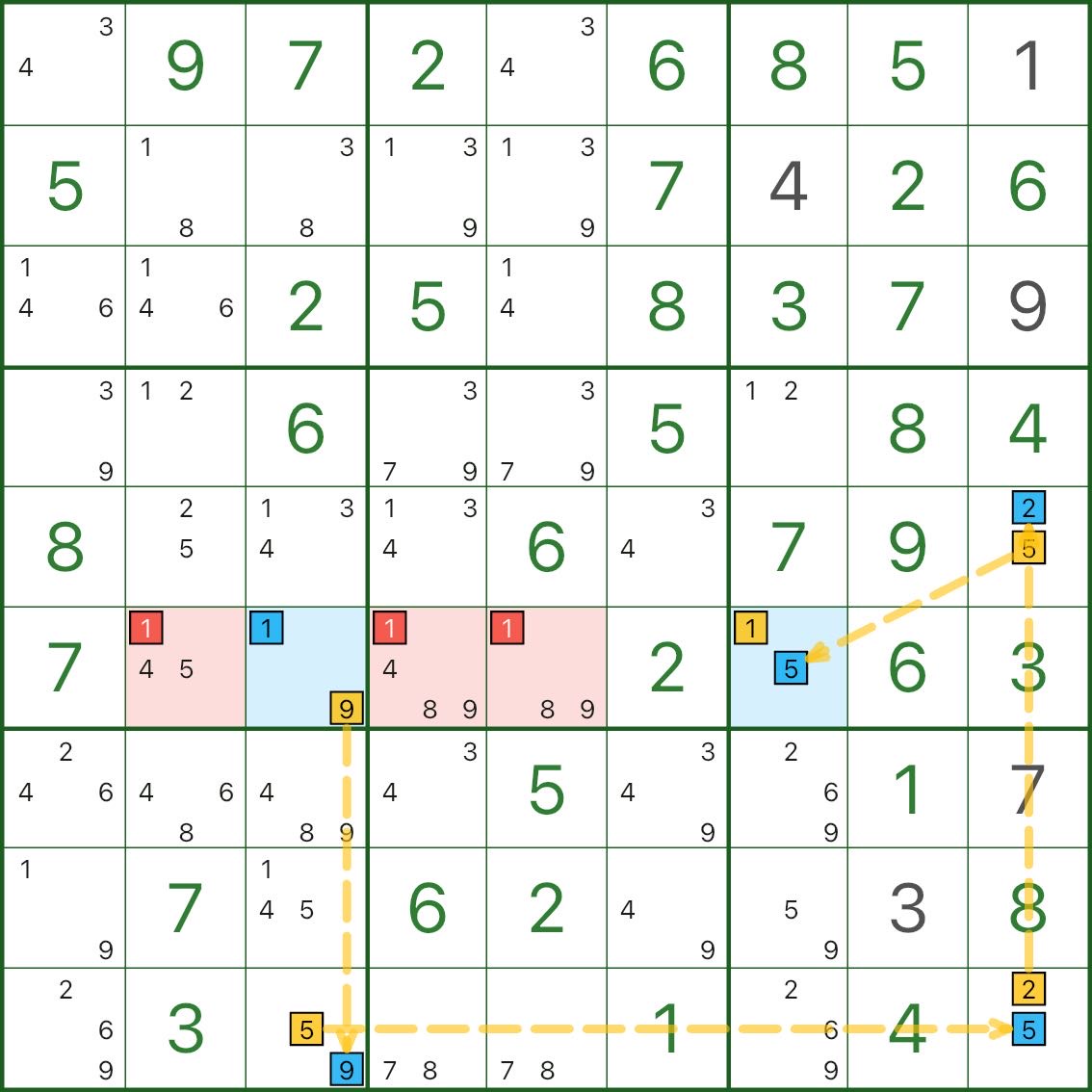
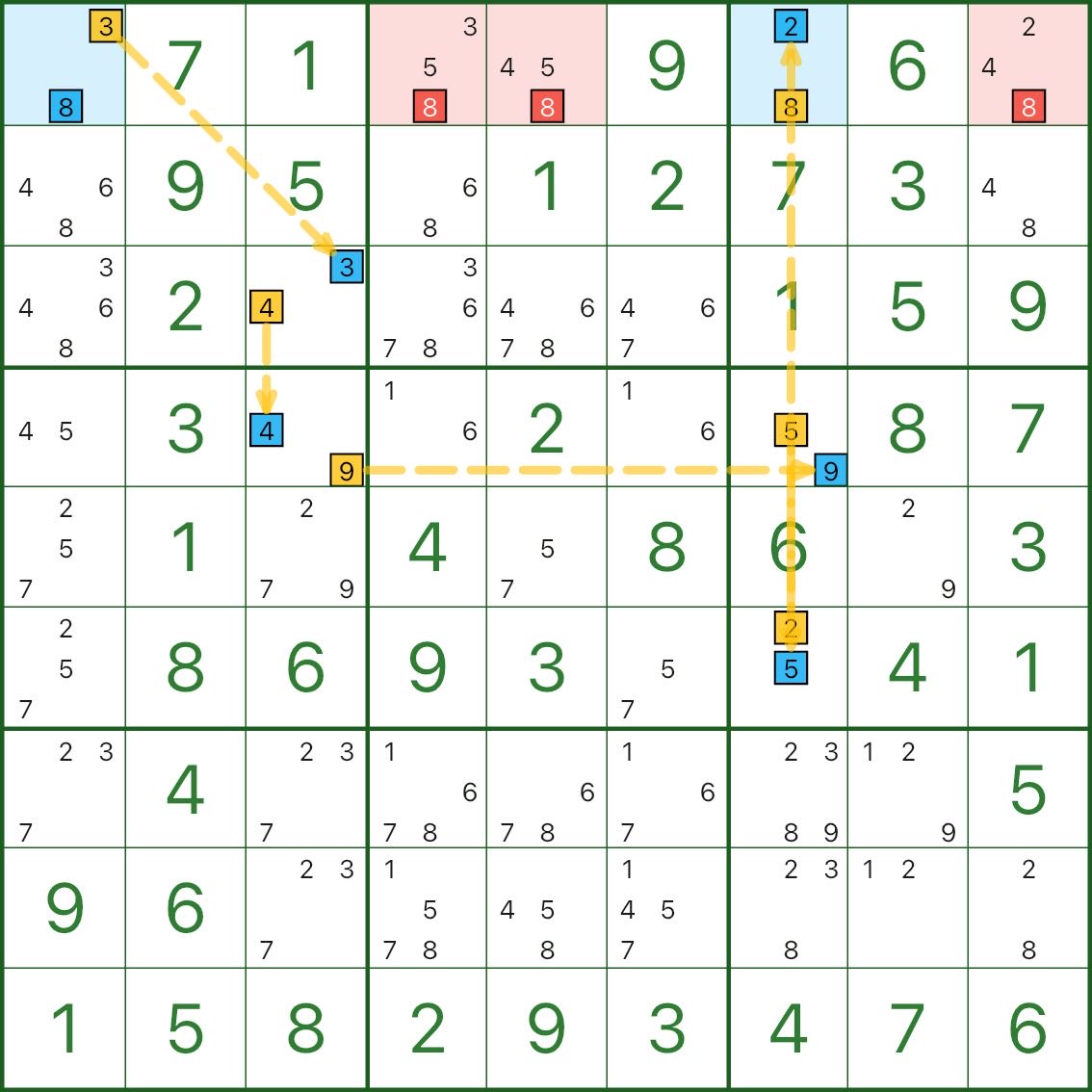
4. How to spot XY-Chain

In one sentence: find a chain of bivalue cells, check whether the two ends land on the same digit d; if a candidate d can see both ends, eliminate it.

Practical checklist:

1. Start from a bivalue cell (exactly 2 candidates)
2. Use “same-digit conflict” (same row/column/box) to link to another bivalue cell
3. Inside each bivalue cell, use the “either X or Y” relationship to keep the inference going
4. If you come back to the same digit d, look for a candidate d that sees both endpoints — that’s a typical elimination