X-Chain

Prerequisite: Chain basics

---

1. Overview

X-Chain is a chain technique that focuses on one digit d.

Think of it as: connect candidate positions of the same digit d using strong links and weak links, to form a “if…then…” reasoning path.

Its most common use is elimination:

• the two endpoints are the same digit d
• if a candidate d can see both endpoints
  ⇒ that candidate d can often be eliminated

---

2. Walkthrough

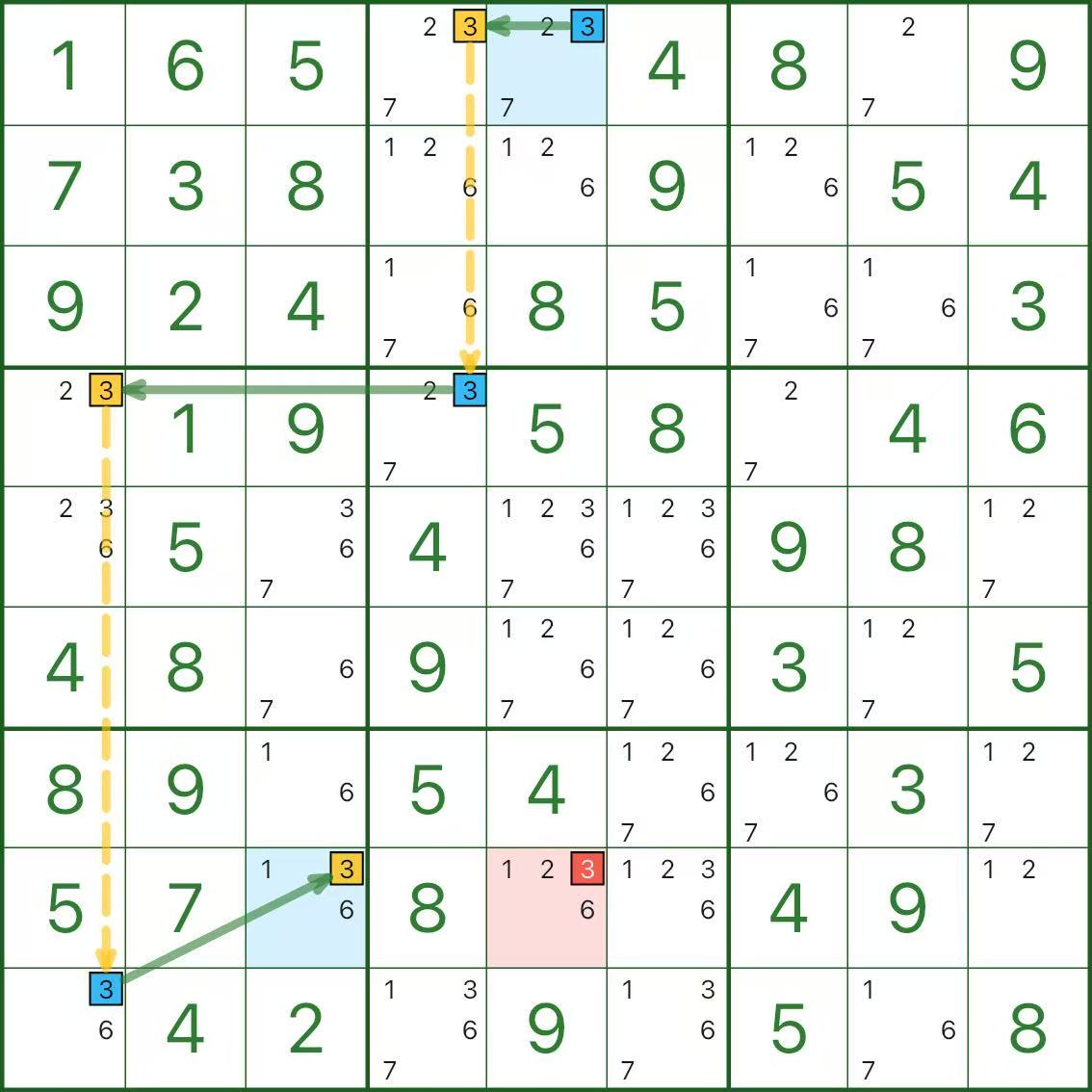
In the image, we only talk about candidate digit 3.

Starting from the blue endpoint r1c5, the chain alternates strong/weak links and eventually reaches the other blue endpoint r8c3.
The red candidate 3 in r8c5 is what we want to eliminate.

Why can we remove 3 in r8c5? A short contradiction is enough:

1. Assume the red candidate r8c5 = 3 is true
2. Then in the same column, r1c5 cannot be 3 (the start becomes “false”)
3. Because the chain alternates strong/weak links:
   • “false” goes through a strong link to force “true”
   • “true” goes through a weak link to force “false”
     step by step, the chain eventually forces r8c3 = 3 (the end becomes “true”)
4. But r8c3 and r8c5 are in the same row: they cannot both be 3 — contradiction

So the assumption is impossible: 3 in r8c5 can be eliminated.

---

3. Examples

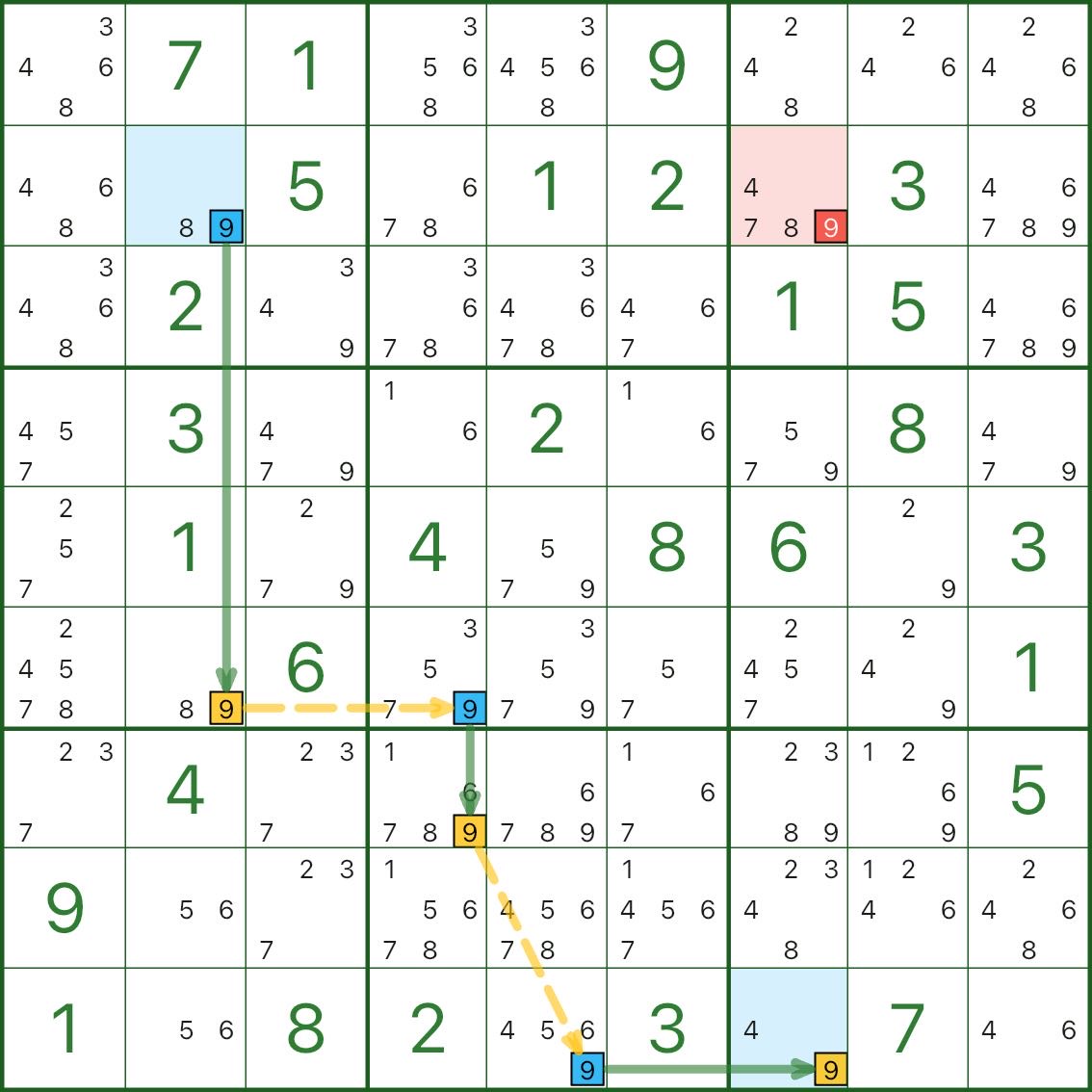
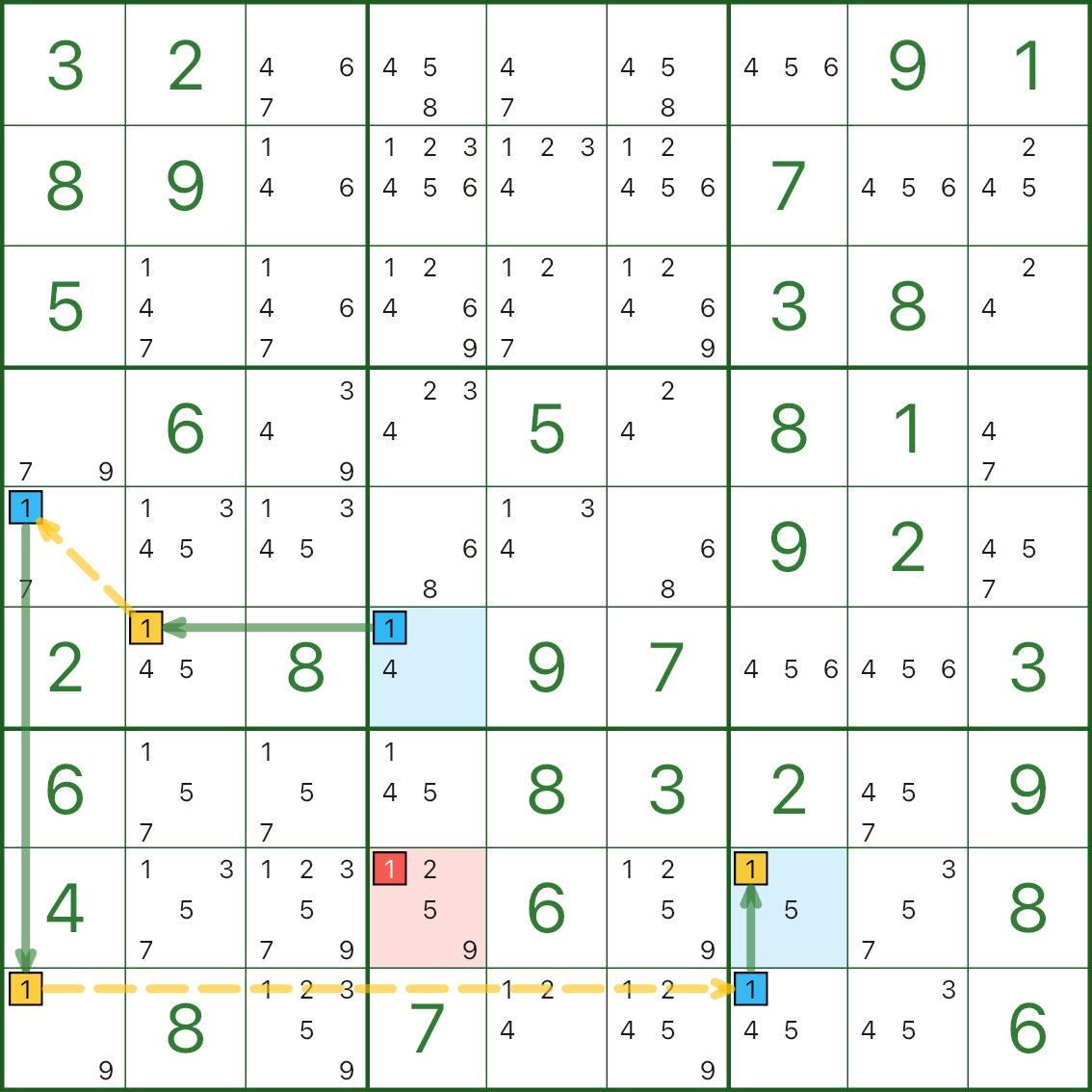
Here are two more X-Chain examples. You don’t need to verify every step at first — train your “pattern eye”:

• focus on one digit d
• find an alternating strong/weak chain connecting two endpoints
• find a red candidate d that can see both endpoints

---

4. How to spot X-Chain

In one sentence: pick a digit d, build an alternating chain using conjugate pairs (strong links), then eliminate d from any cell that can see both endpoints.

Practical checklist:

1. Pick a digit d (for example 3)
2. In rows/columns/boxes, find places where d has exactly two candidate positions (that’s a strong link)
3. Connect these segments using “can see each other” relations (weak links) to form an alternating chain
4. Find a candidate d that can see both endpoints — that’s a typical elimination