WXYZ-Wing

If you’ve already read these, WXYZ-Wing will feel much easier:
XY-Wing / XYZ-Wing

---

1. Overview

WXYZ-Wing is basically a “bigger” version of XY-Wing / XYZ-Wing: we use a small structure to force a clear contradiction, and then eliminate a candidate.

On the board it usually looks like a small colored cluster (a blue hub cell + yellow wing cells):

• all candidates in this cluster are limited to 4 digits (for example {1,4,7,9})
• if we assume a red candidate d is true, it removes d from other places in the cluster
• then the cluster has only 3 digits left to fill 4 cells
  • ⇒ at least one cell will have no valid value (contradiction)

So the red candidate d can be eliminated.

---

2. Walkthrough

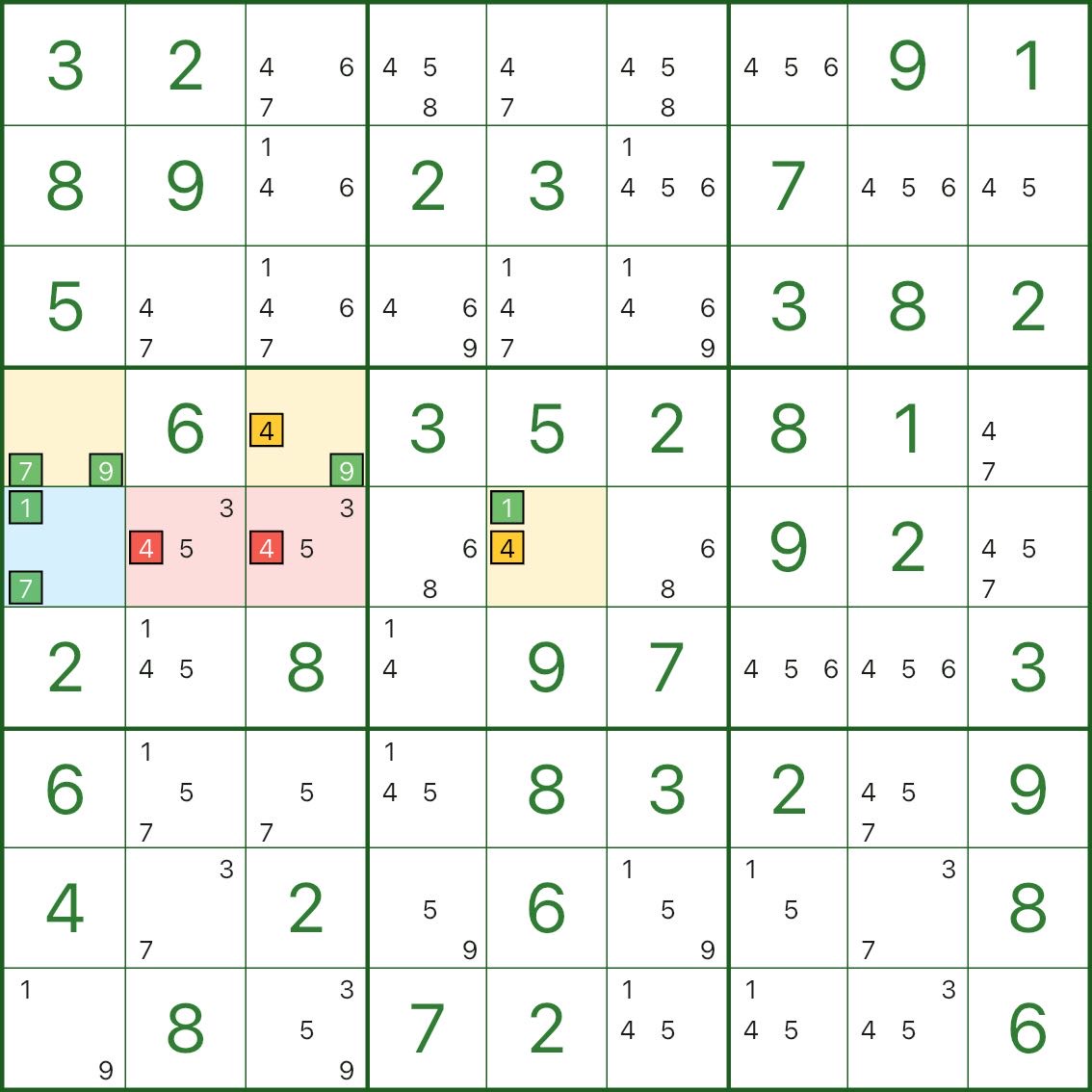
In the image: blue is the hub cell, yellow are the wings, and red are the eliminations.
We are removing candidate 4 in the two red cells (r4c2 and r4c3).

Why can the red 4 be removed? A short contradiction is enough:

• assume the red candidate 4 is true
• then any conflicting 4 in the yellow wings must be removed
• the wings become forced to distribute only among 1, 7, 9 (those digits are already highlighted in the image)
• but the blue hub cell also only has 1, 7 available
  once the wings “use up / block” 1, 7, 9 against the hub, the hub cell is left with no valid value (contradiction)

So the assumption is impossible: the red candidate 4 can be eliminated.

---

3. Examples

Here are two more WXYZ-Wing examples. You can simply compare the structure: blue hub / yellow wings / red eliminations.

---

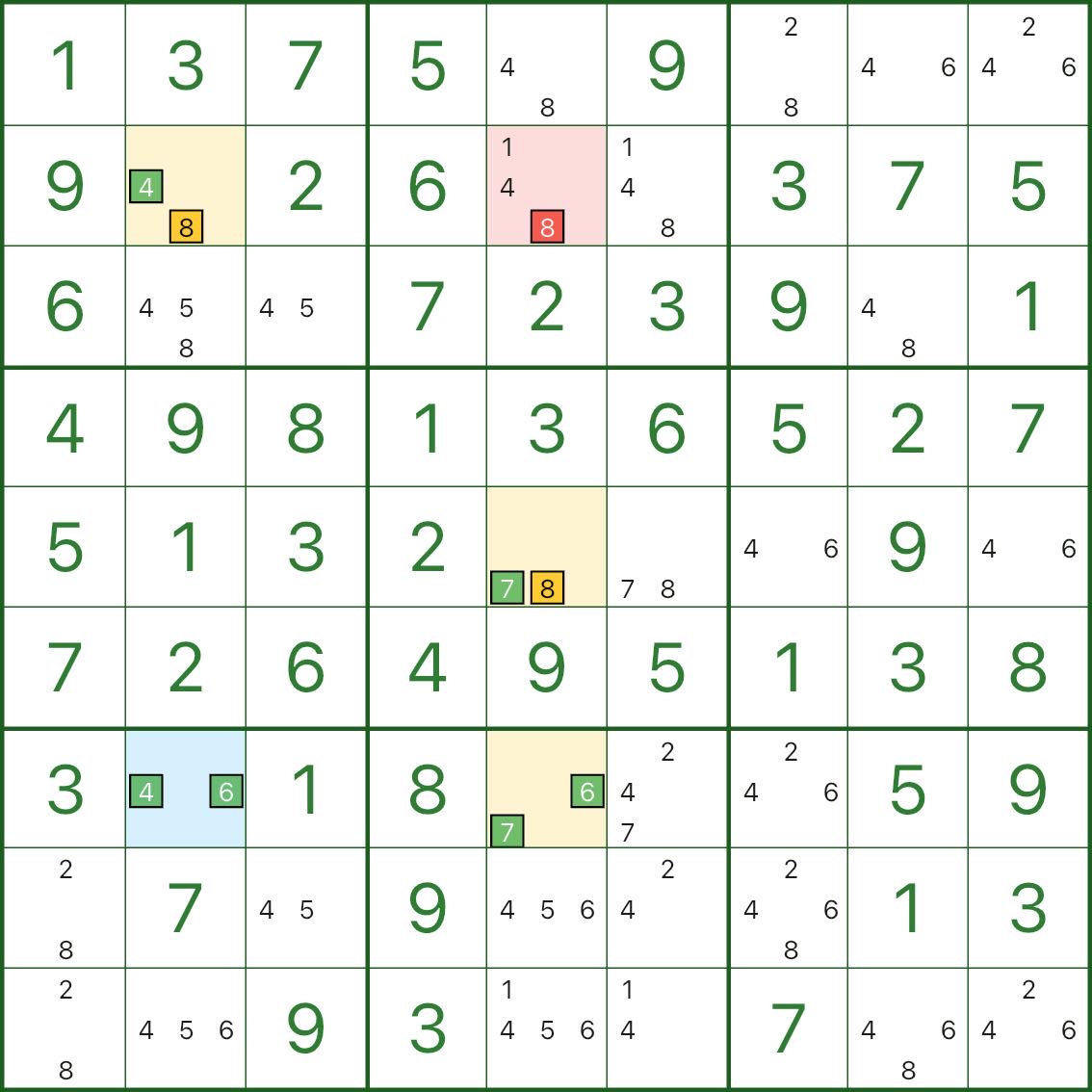
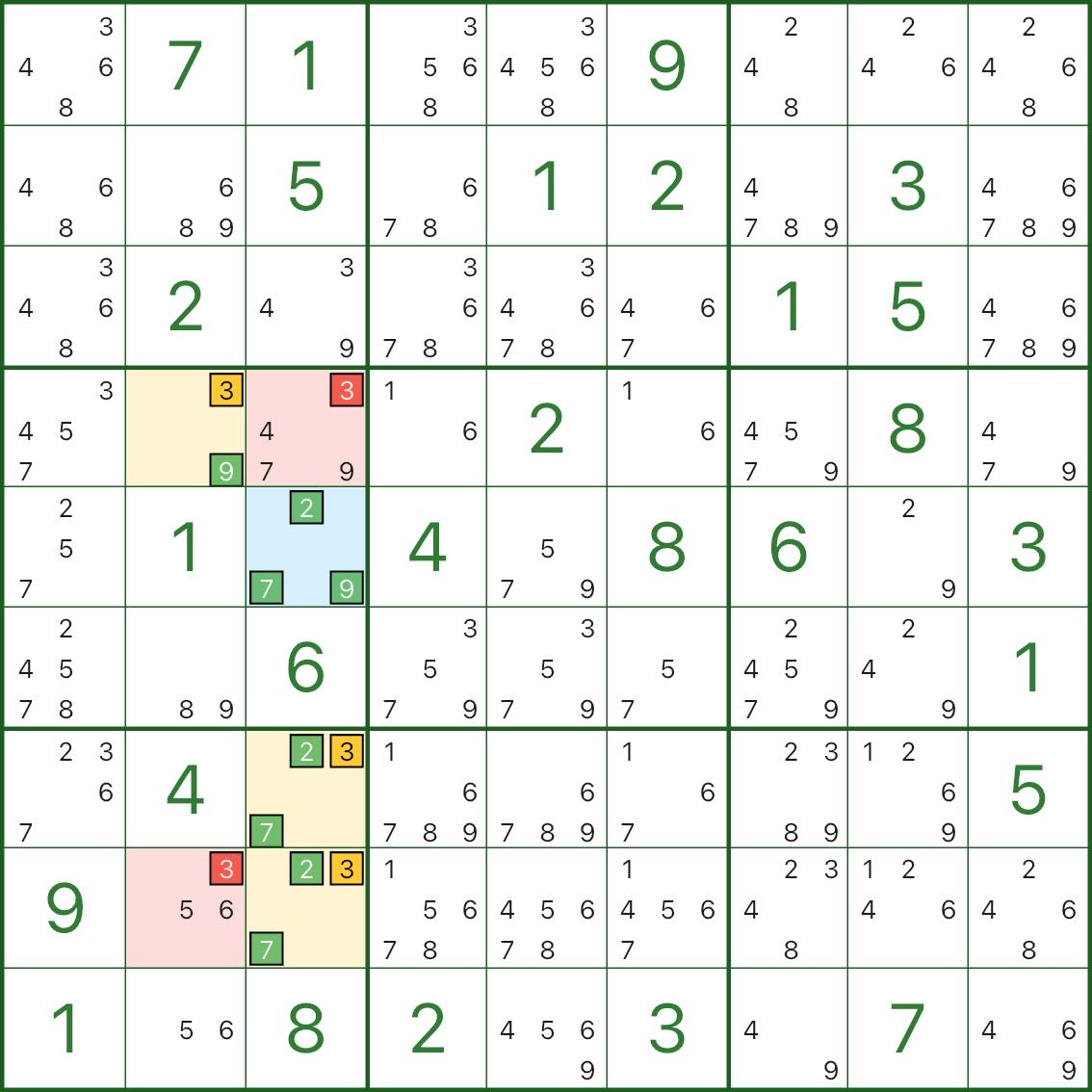
4. How to spot WXYZ-Wing

In one sentence: find a blue/yellow cluster limited to 4 digits, then test the red candidate with a quick contradiction — if it makes the cluster leave some cell with no value, it can be eliminated.

In practice:

1. Look for a small colored cluster (blue + yellow) where the cells can see each other locally
2. Check whether all candidates in that cluster are limited to 4 digits
3. Look at the red candidate: if assuming it true “pushes out” a digit and makes some colored cell have no value, you have the elimination
4. Eliminate it