W-Wing

Description

W-Wing is a short candidate elimination technique. It usually starts from two matching two-candidate cells (often called the two wings).

The core intuition is:

• Both wings have the same two candidates (for example {a, b})
• If some candidate b is assumed true, it removes b from both wings
• Then both wings are forced to a, which creates a contradiction in some row/column/box

So candidate b can be eliminated.

---

Explanation

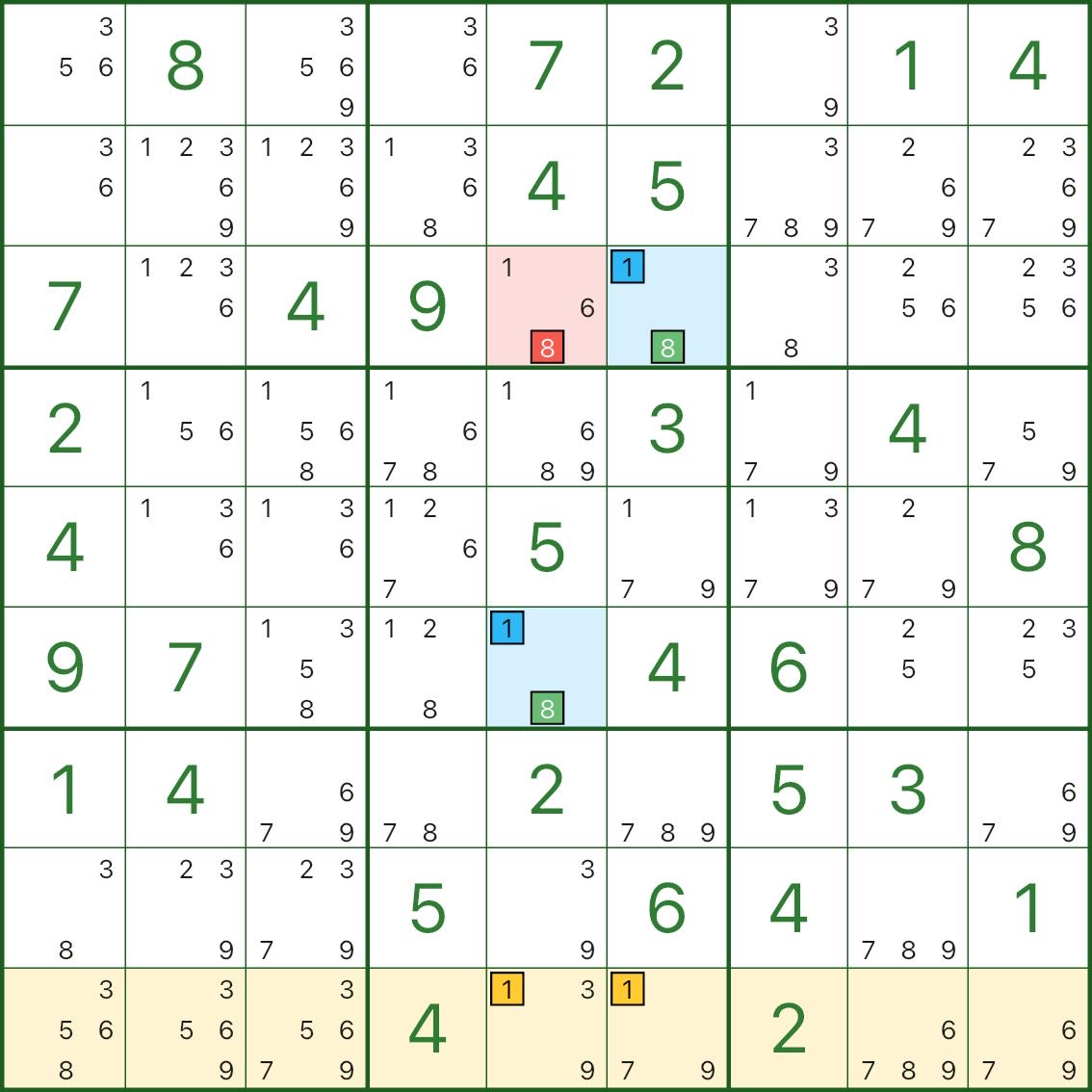
In the image above, we want to eliminate candidate 8 in r3c5 (red).
The two wings are r3c6 and r6c5. Both are two-candidate cells with 1 and 8.
The yellow highlight marks row 9, showing the contradiction: if both wings become 1, row 9 has no place left for digit 1.

Why can we remove 8 from r3c5? A short contradiction is enough:

• Assume r3c5 = 8 (the red candidate is true)
• r3c5 can see both wings, so 8 is removed from both wings:
  • r3c6 must be 1
  • r6c5 must be 1
• Now row 9 is “blocked”: all places for digit 1 in the yellow row conflict with those two 1s, so row 9 has no place for 1 (contradiction)

So the assumption is impossible: r3c5 cannot be 8, and candidate 8 can be eliminated.

---

Examples

These images show more W-Wing patterns. Try to spot the same structure: two wings / an elimination cell / a contradiction unit.

---

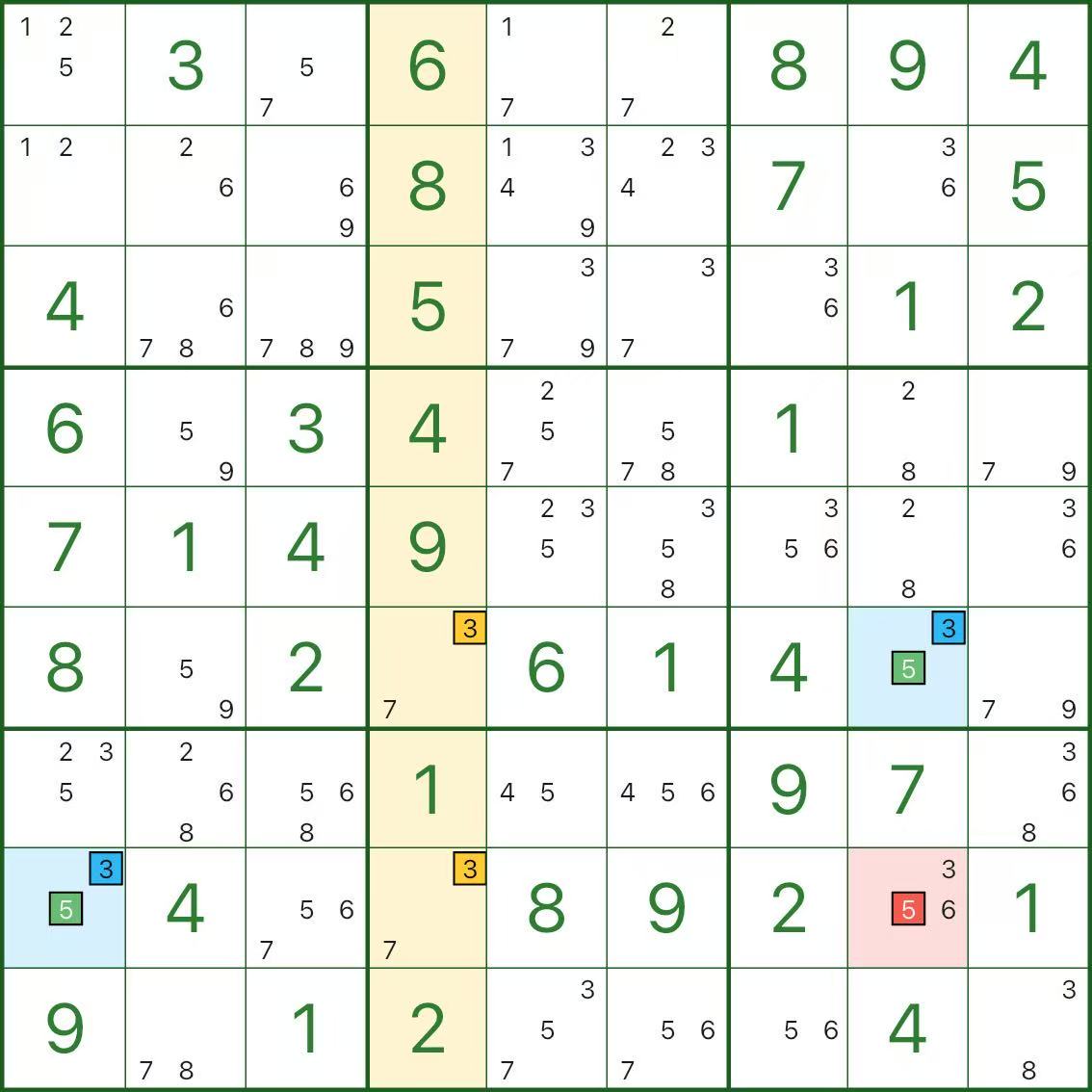
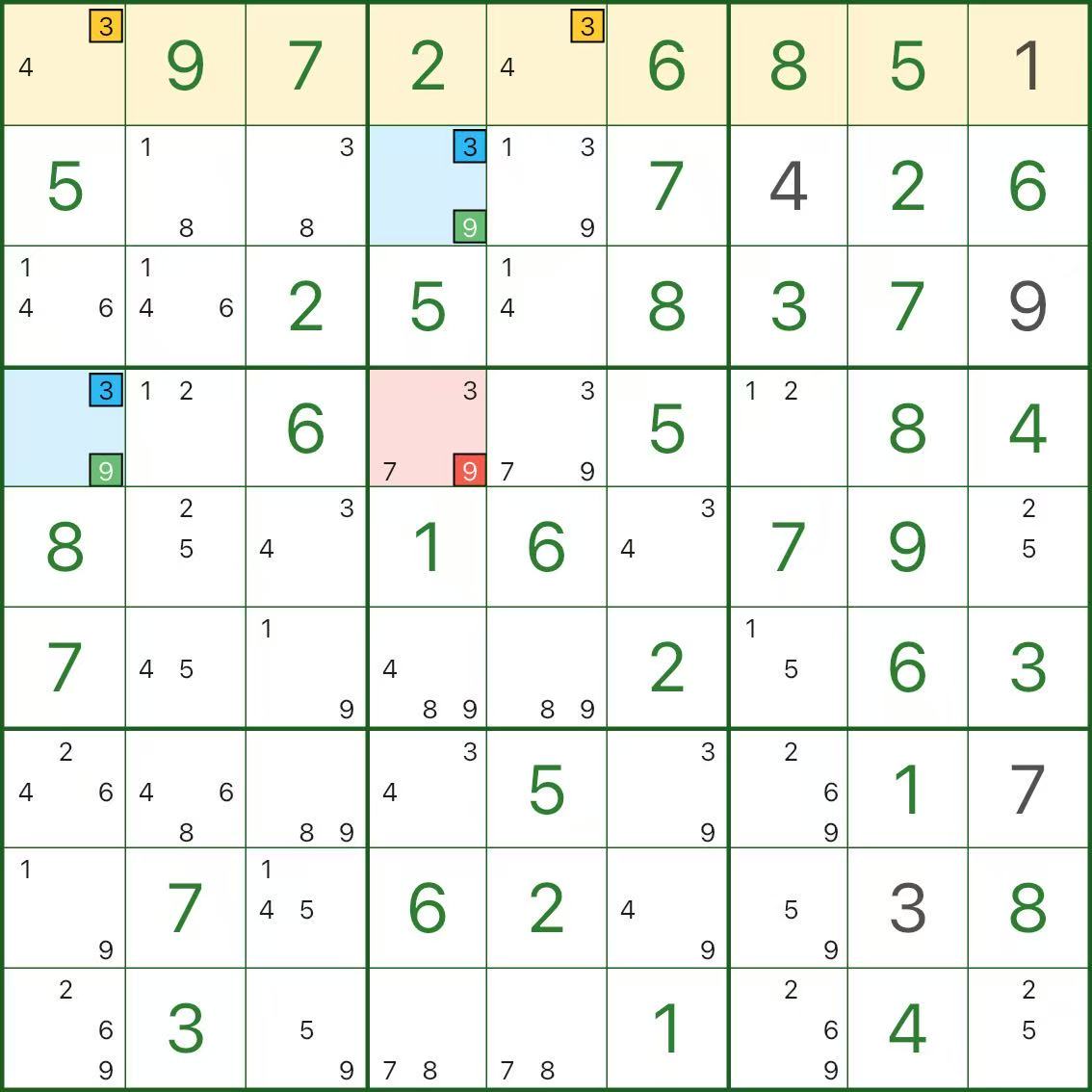
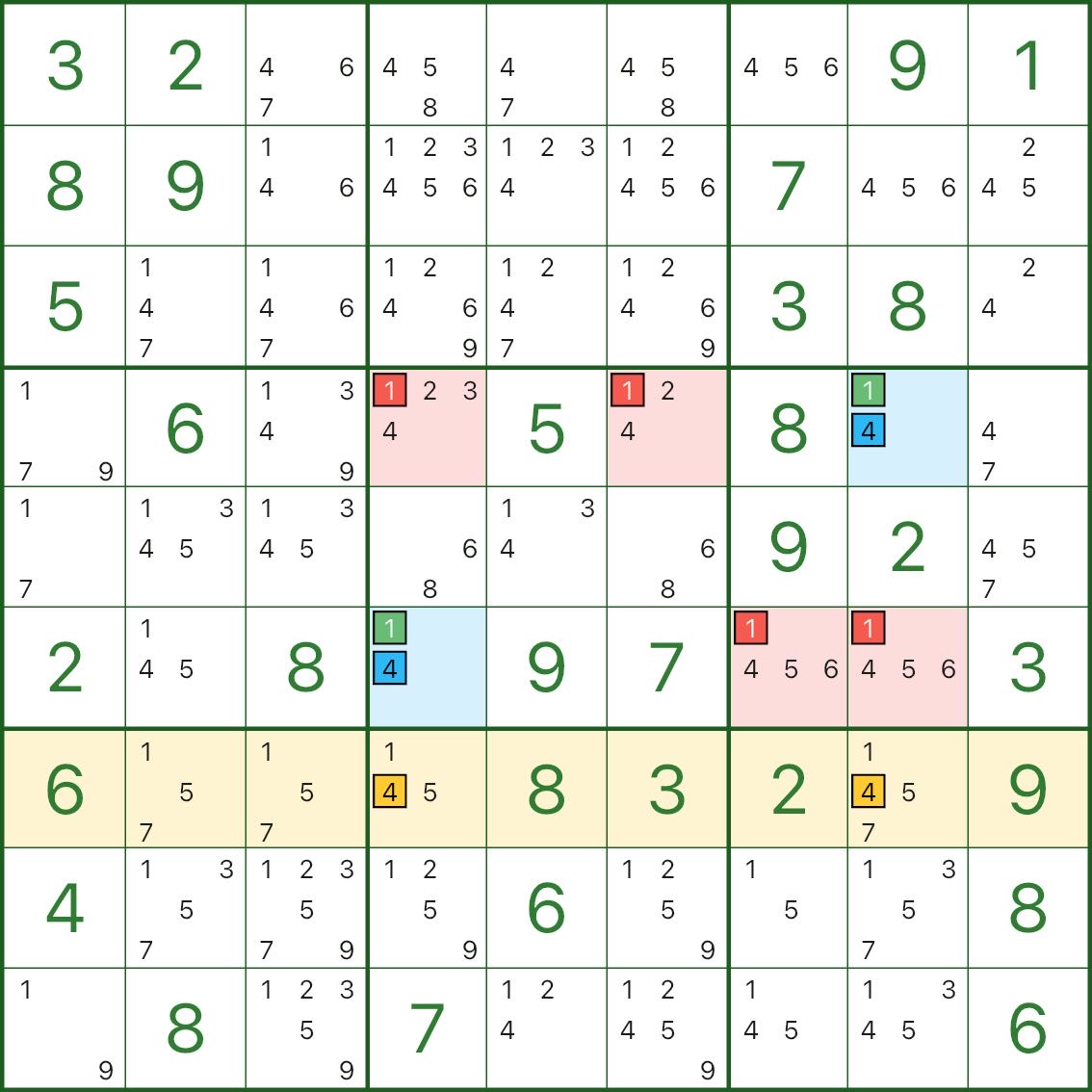
How to Find W-Wing

One-line checklist: find two matching two-candidate wings, find an elimination spot that sees both wings, then confirm forcing both wings to the same digit creates a contradiction.

In a real puzzle:

1. Find two two-candidate cells with exactly the same pair (the wings)
2. Find a cell that can see both wings and contains one of the wing digits (often the elimination candidate)
3. Do a quick contradiction check: assume that candidate is true → both wings are forced to the other digit → some row/column/box ends up with no place for that digit
4. If the contradiction holds, eliminate the candidate