Unique Solution

1. No conflict ≠ correct

Many beginners think:

“This number doesn’t appear in the row, column, or box—so I can place it.”

It sounds reasonable, but it’s often wrong.

Why?

Because Sudoku isn’t “pick any number that is legal right now”.
It’s a logic puzzle designed to have one complete solution.

So the number you place:

• may not conflict immediately
• but it can still force a future row / column / box into a dead end

That’s why in this app you may see:
no visible conflict yet, but the move is still marked as wrong.

It’s not because the board conflicts now—it’s because:
that value cannot belong to the puzzle’s unique solution.

---

2. An example: looks legal, but leads to a dead end

Let’s walk through a small example with images.

Step 1: r6c6 seems like it could be 1

Look at the highlighted cell r6c6. In its row, column, and box, there is no 1.
So you might think: let’s place 1 here.

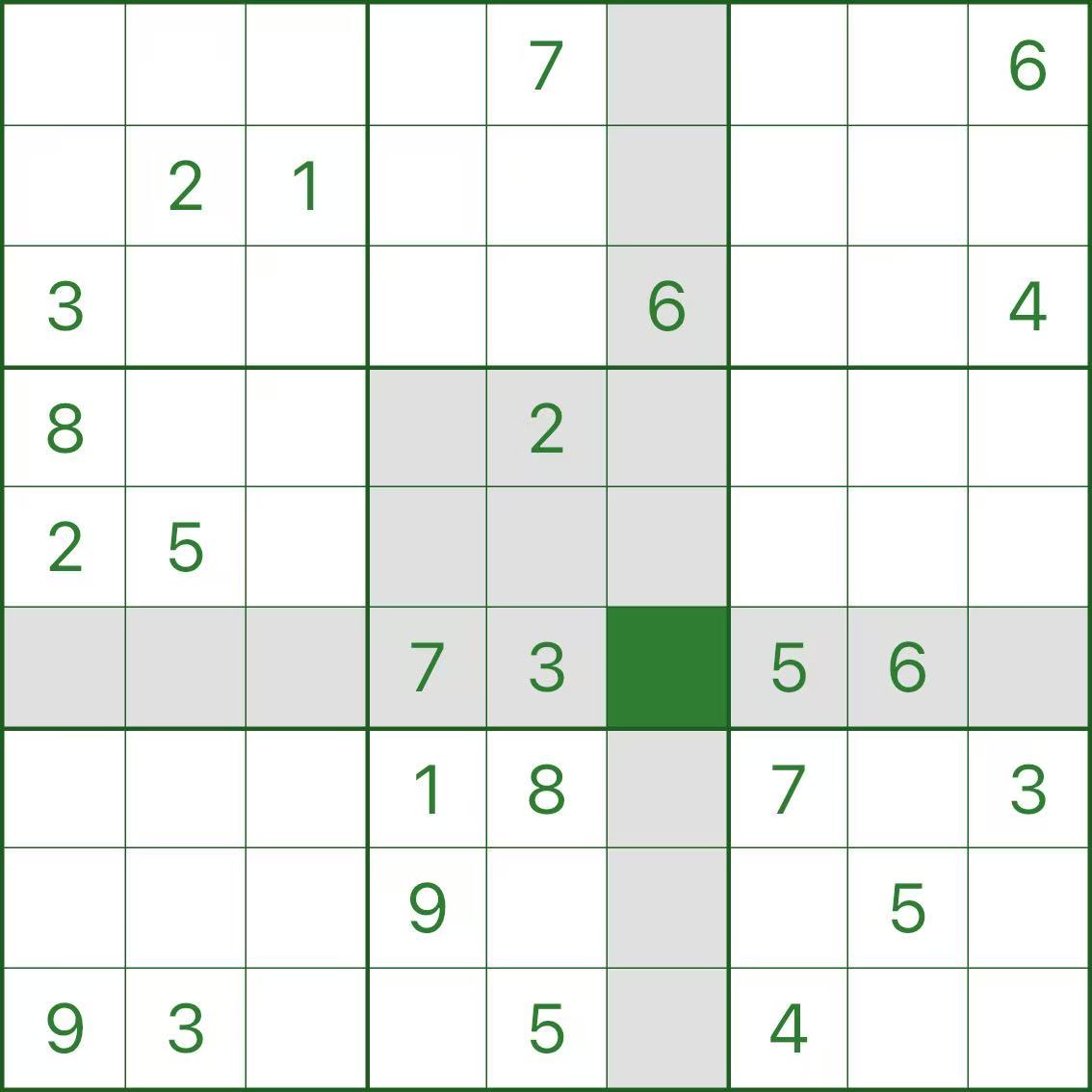
Step 2: r6c1 is forced to be 4

Now check the highlighted cell r6c1.
If you cross out the digits that already appear in its row, column, and box, only one option remains: 4.

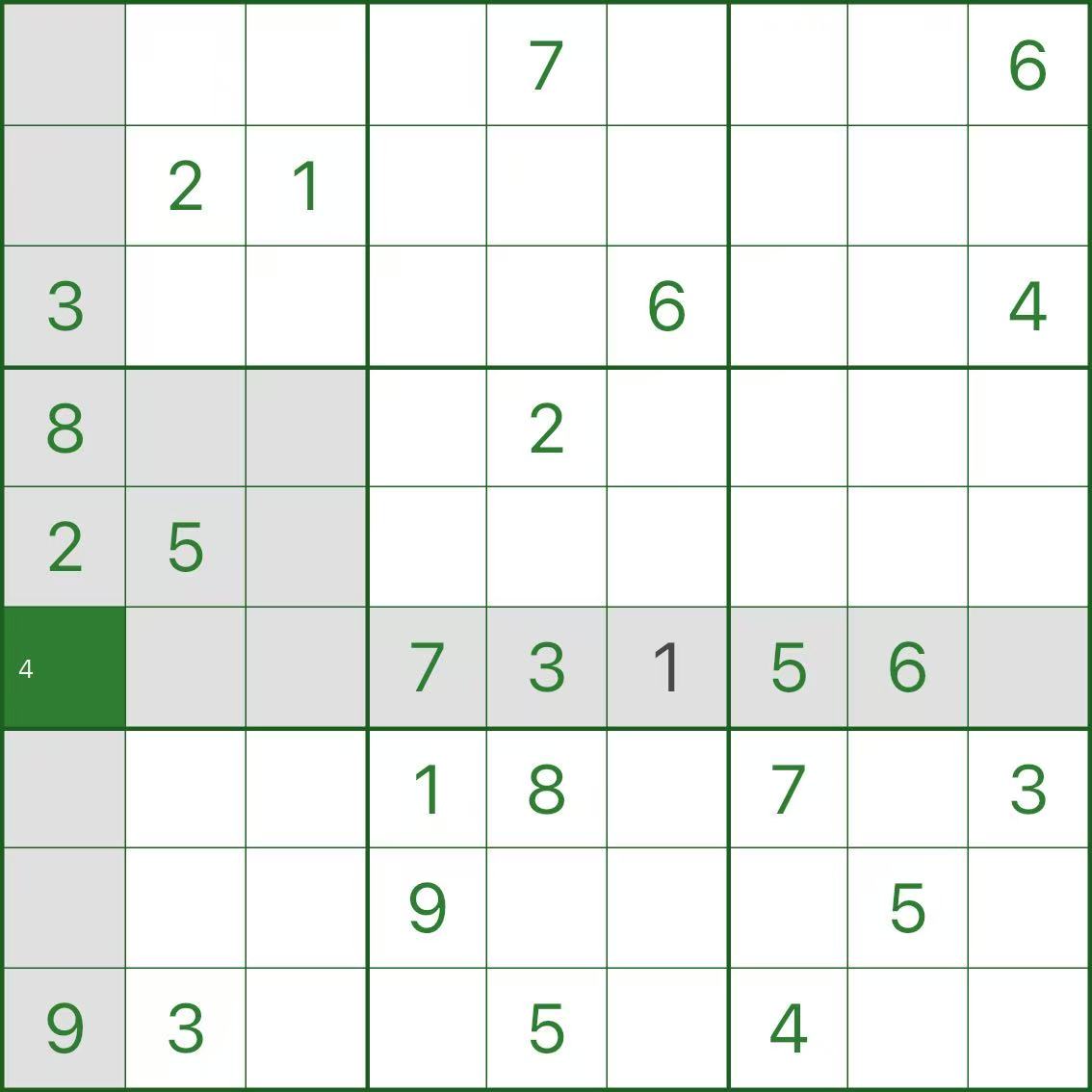
Step 3: r6c2 is forced to be 9

Next, look at r6c2. Do the same elimination, and you’ll find only one option remains—9.

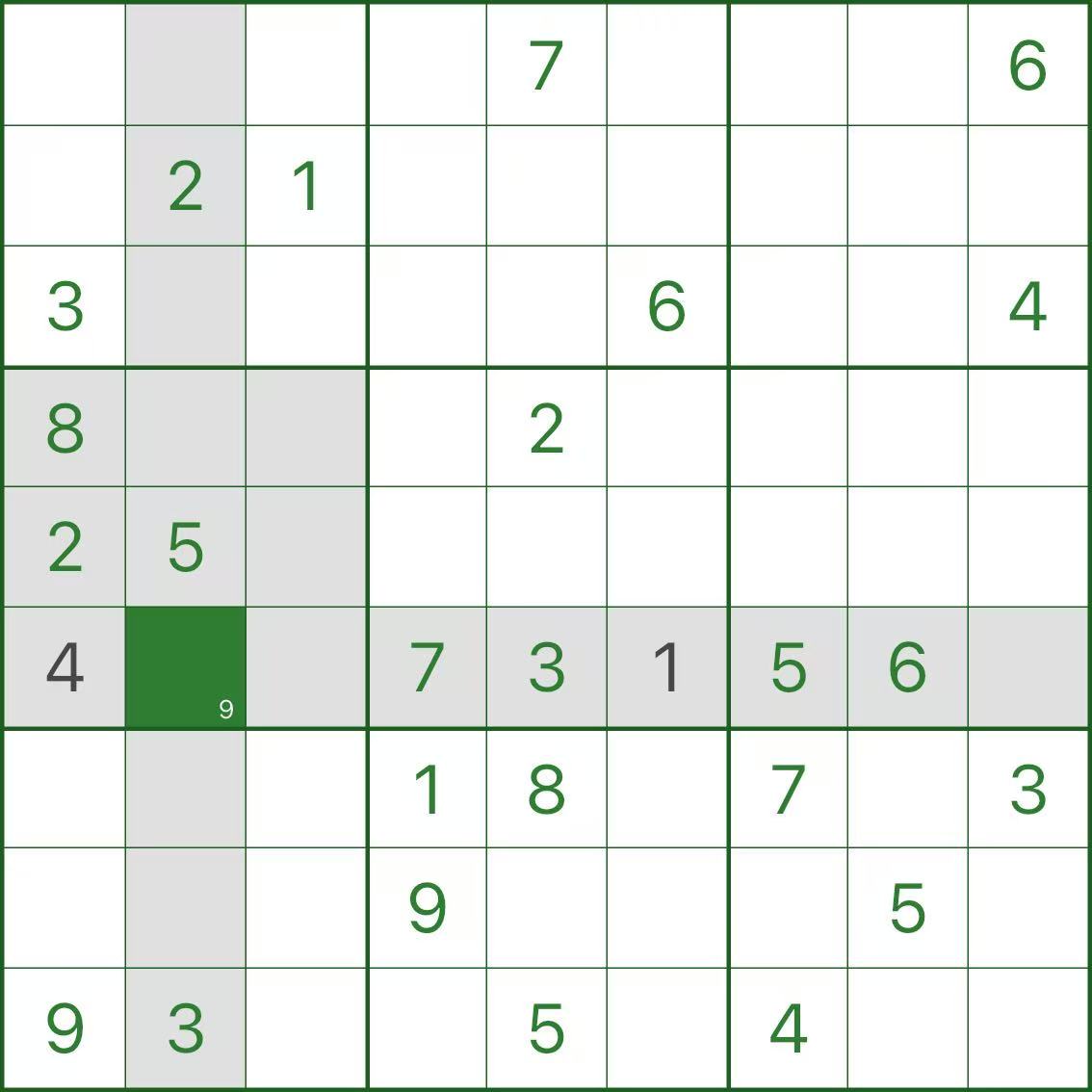
Step 4: r6c3 ends up with no possible number

Now we reach r6c3. You’ll see that:
every digit from 1 to 9 is blocked by its row/column/box, so nothing can be placed there.

In other words, the first “no-conflict” move eventually pushed the puzzle into a dead end.

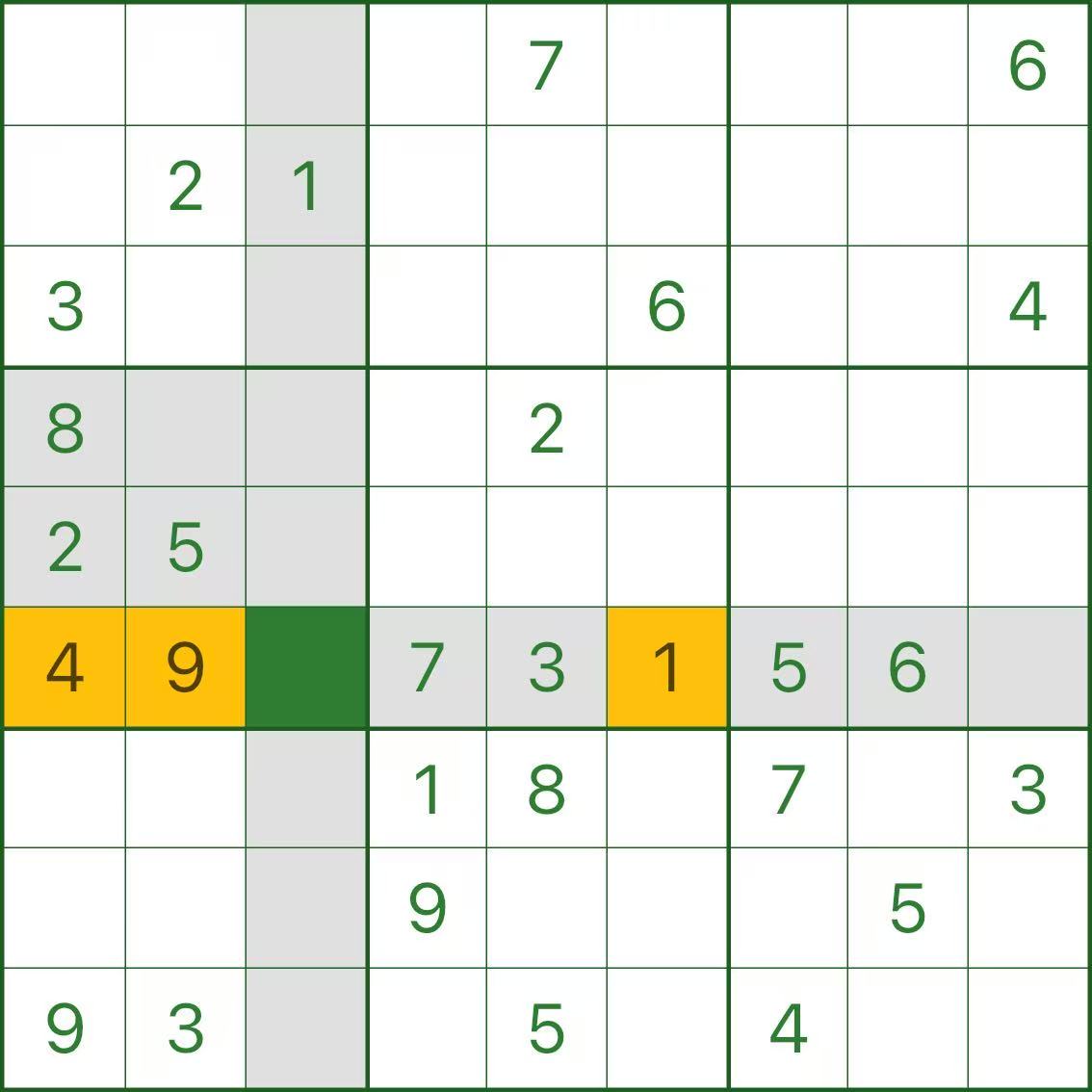
Reference: the correct solution

Here is the correct solution for this puzzle so you can compare:

---

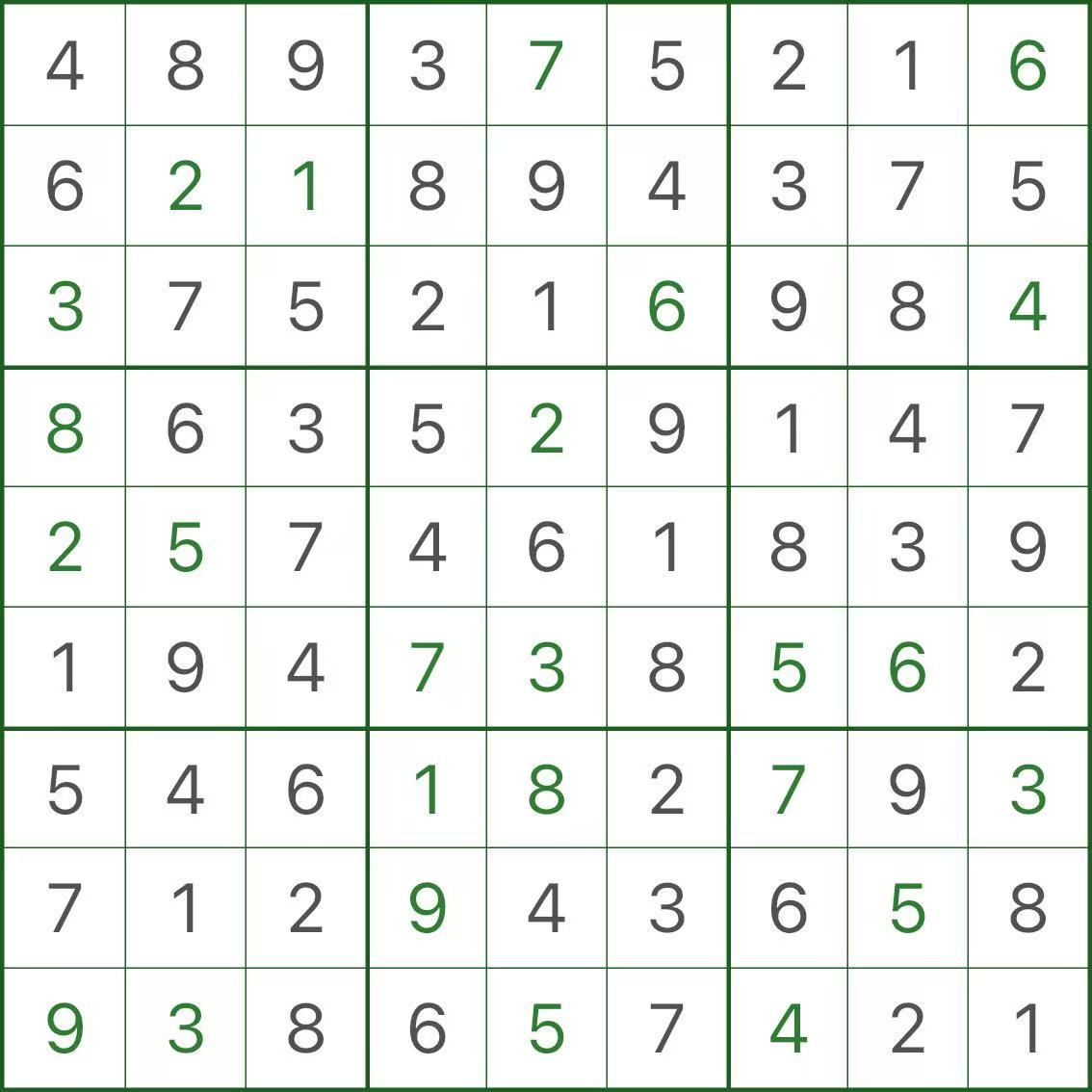
3. The right mindset: prove “must”, not just “can”

The most important habit in Sudoku is:

Don’t place a number just because it can go there.
Place it only when you can prove it must go there.

When you’re not sure, do this instead:

• write down pencil marks (possible candidates)
• use elimination and other techniques to reduce candidates step by step
• until a cell has only one candidate left, or a digit has only one place in a row/column/box

This keeps every move explainable—and makes it much clearer why a hint is valid.