Unique Rectangle (UR)

Prerequisite: UR relies on the fact that the puzzle has exactly one solution.
If you haven’t read it yet, start here:
Uniqueness

---

1. Overview

Unique Rectangle (UR) is a family of techniques that uses the single-solution property to eliminate candidates (and sometimes place a number).

It focuses on a “dangerous shape”:

• four cells form a 2×2 rectangle (two rows × two columns, spanning exactly two boxes)
• all four corners contain the same two core candidates (for example, 1 and 7)

If we leave those four cells with only that pair, the rectangle can often be filled in two different ways (by swapping the two digits), which would break uniqueness.
So under the uniqueness assumption, we can conclude: some candidates must be removed, or a cell must take a specific value.

---

2. Walkthrough (5 types)

The 5 images below correspond to the 5 common UR types (the in-app hints label them as Type I–V).

Color guide:

• Blue cells: the UR rectangle (the core structure)
• Yellow marks: candidates we’re focusing on in the reasoning
• Red marks: candidates to eliminate / or a cell that can be set

Type I: single roof → a forced value

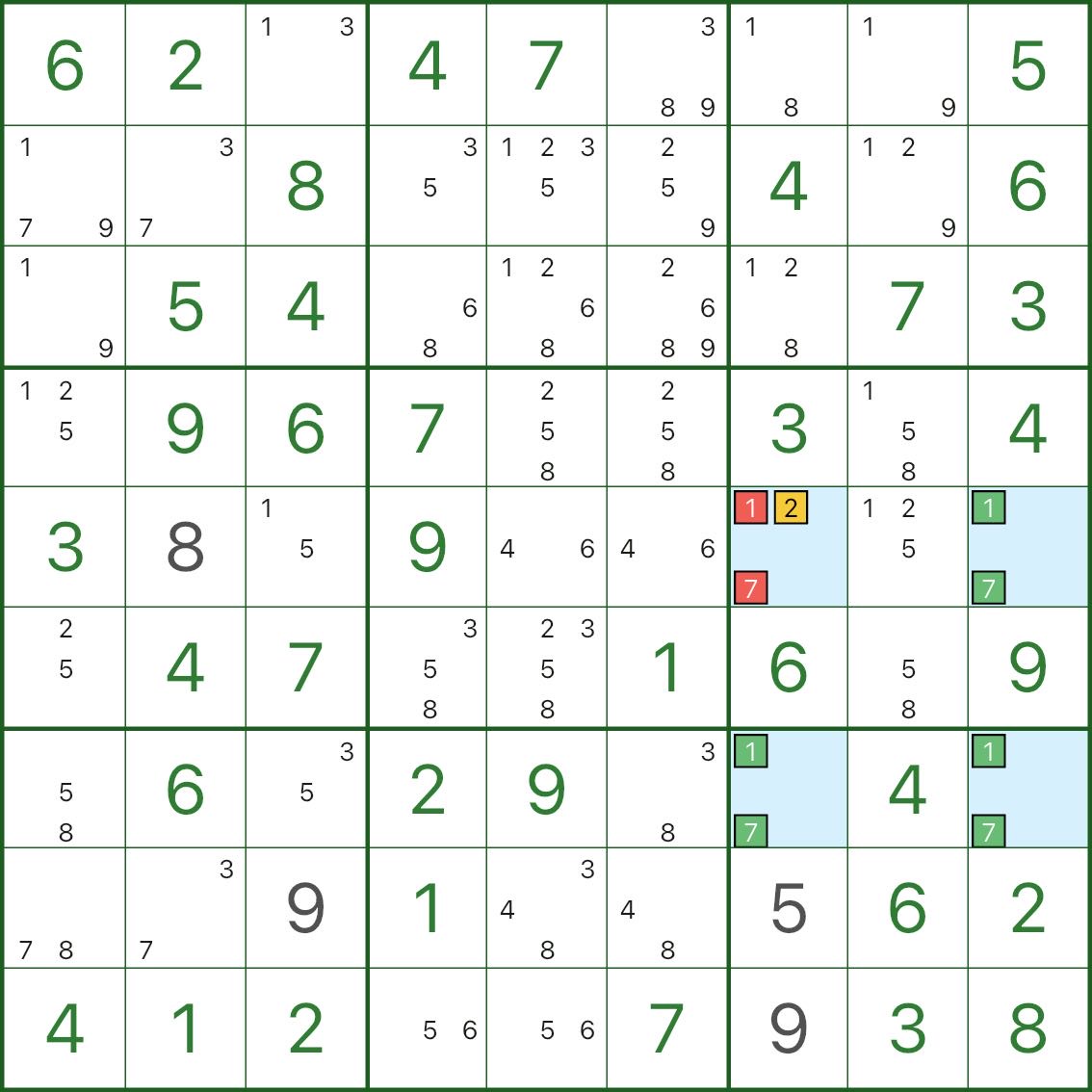
Look at the four blue cells: they form a rectangle and all contain candidates 1 and 7.
Cell r5c7 also has an extra candidate 2.

If 2 is not true in r5c7, then r5c7 would be left with only 1 and 7.
That would make all four corners “{1,7} only”, allowing two swap-able fillings (breaking uniqueness).

So under uniqueness:

• r5c7 cannot keep candidates 1 and 7
• therefore r5c7 must be 2

---

Type II: two roofs → eliminate c that sees both roofs

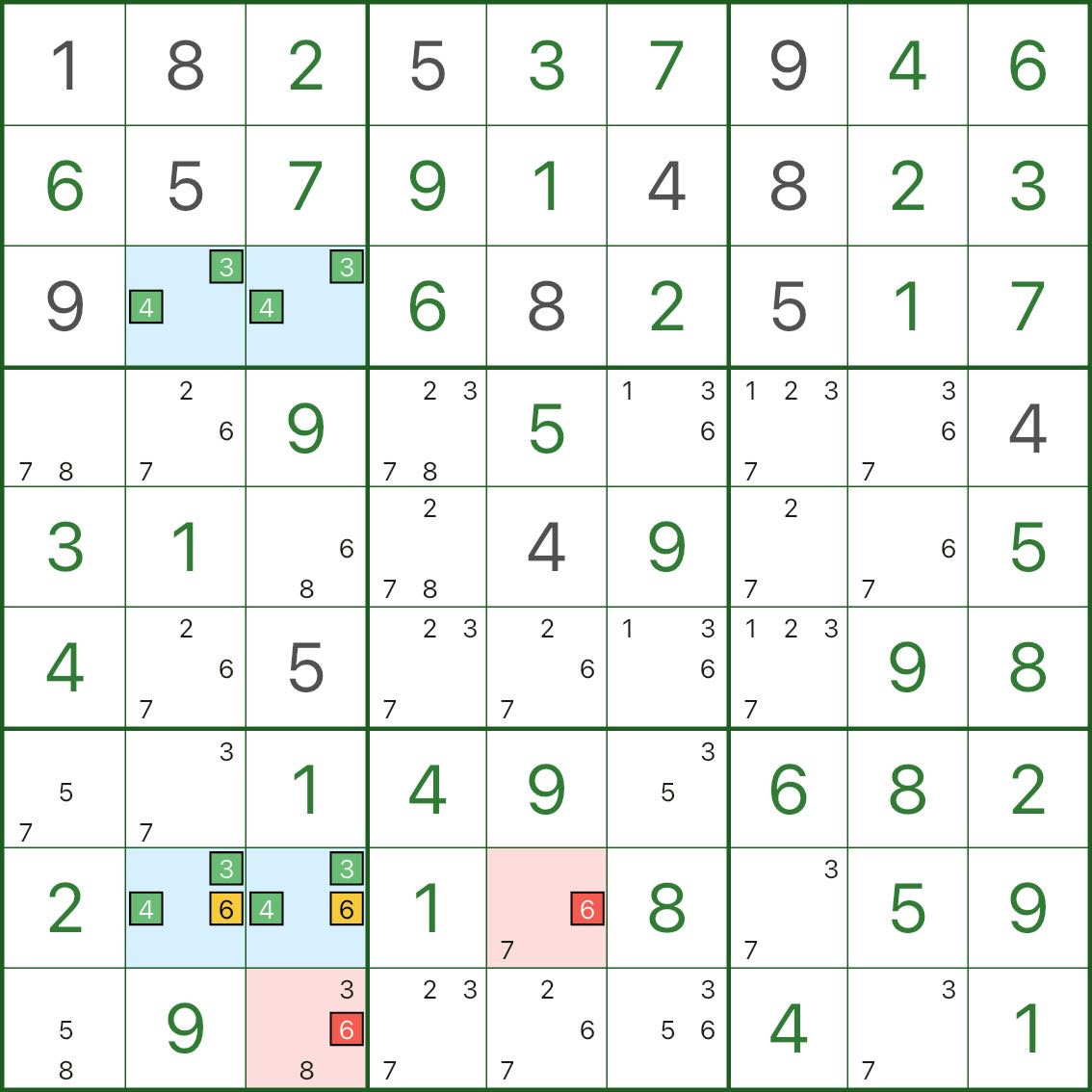
Here the blue rectangle is based on core candidates 3 and 4.
Two blue cells r8c2 and r8c3 also contain candidate 6 (so they are {3,4,6}).

Now consider a red candidate 6 (for example in r8c5 or r9c3) that can see both roof cells:

• if that red 6 were true, both roofs would be forced not 6
• the roofs would collapse back to {3,4} only
• the rectangle becomes a deadly {3,4} pattern again (breaking uniqueness)

So those red 6 candidates cannot be true and can be eliminated.

---

Type III: treat the roofs as a “package” and form a subset

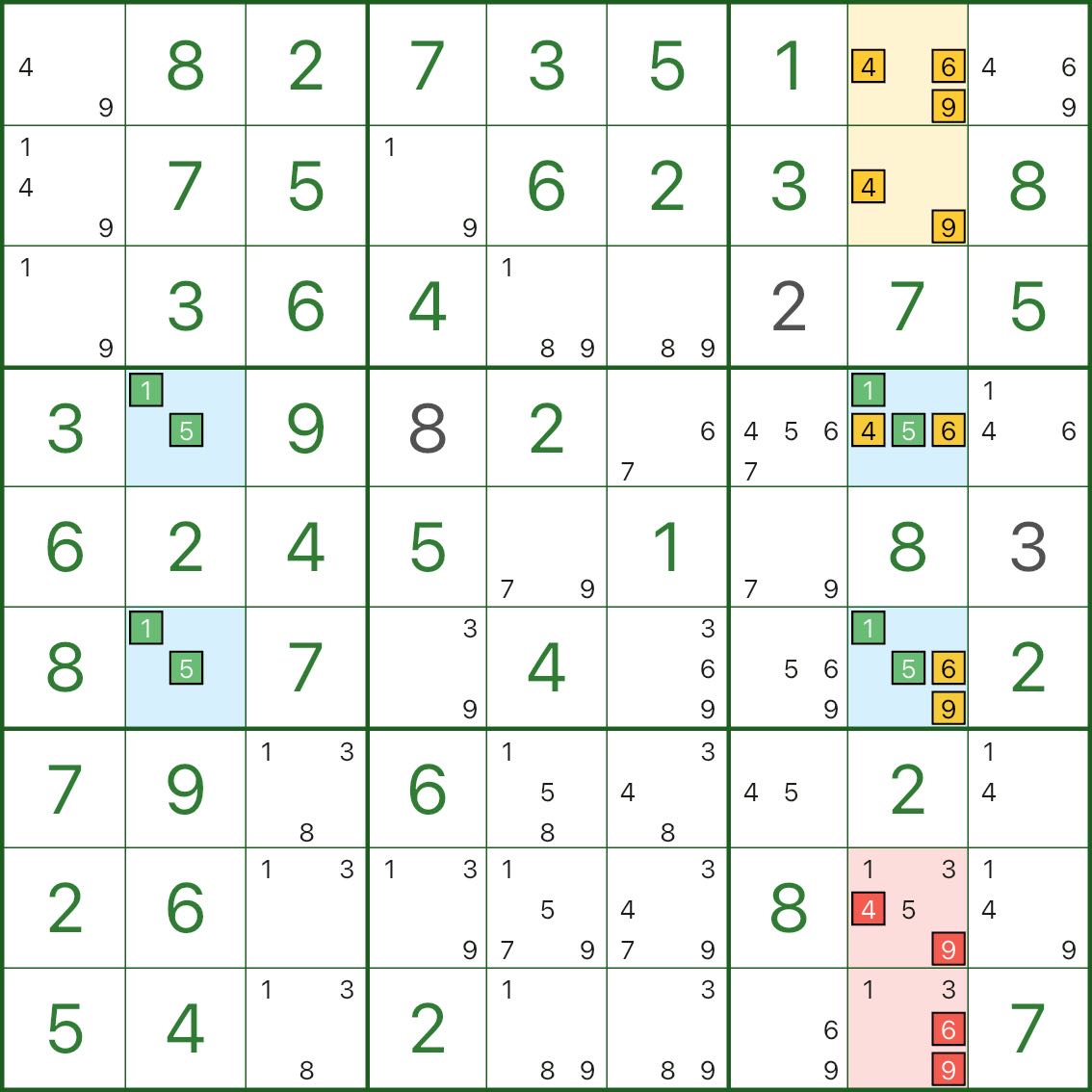
This one focuses on column 8:

• two blue cells in column 8 both contain core candidates 1 and 5
• they also share extra digits 4, 6, 9 (so each is {1,5,4,6,9})

Uniqueness forces an important constraint:

• among those two blue cells, at least one must take a digit from {4,6,9}
• otherwise both would rely only on {1,5}, turning the rectangle into a deadly pattern

So we can treat “the extra digits {4,6,9} of the two blue cells” as a package.
Together with the yellow cells r1c8 and r2c8, this effectively locks digits 4, 6, 9 inside a small subset in column 8.

Therefore, any other 4/6/9 candidates in column 8 (marked in red) can be eliminated.

---

Type IV: a conjugate pair forces one digit → eliminate the other

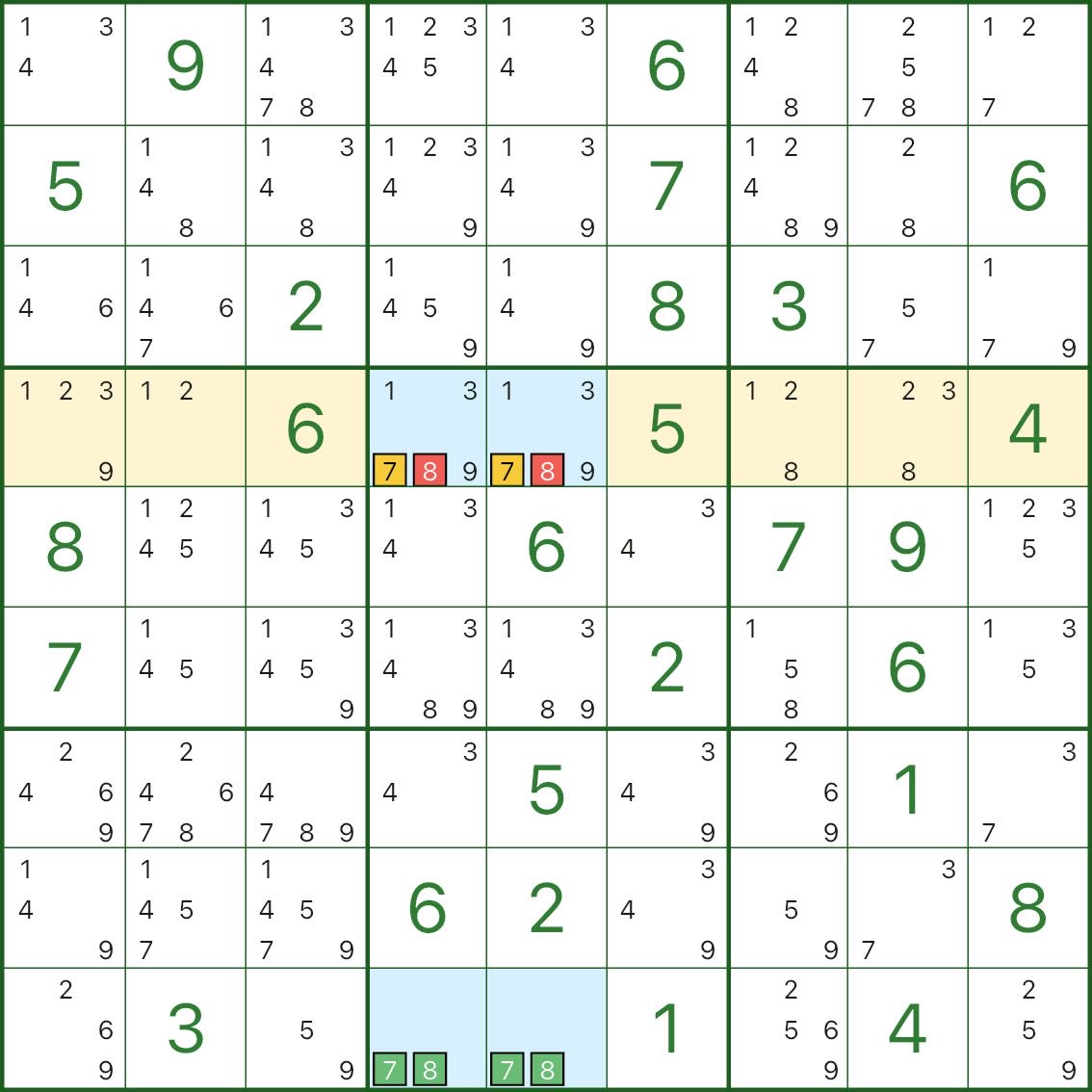
The blue rectangle is built on a core pair again (here 7 and 8).

In row 4, candidate 7 appears only in the two blue cells r4c4 and r4c5.
That means:

• one of r4c4 / r4c5 must be 7

With this constraint, keeping candidate 8 in those same blue cells would still allow the rectangle to collapse into a deadly structure (breaking uniqueness).

So we can eliminate 8 from r4c4 and r4c5.

---

Type V: multiple roofs (2 or 3) → eliminate c that sees all roof cells

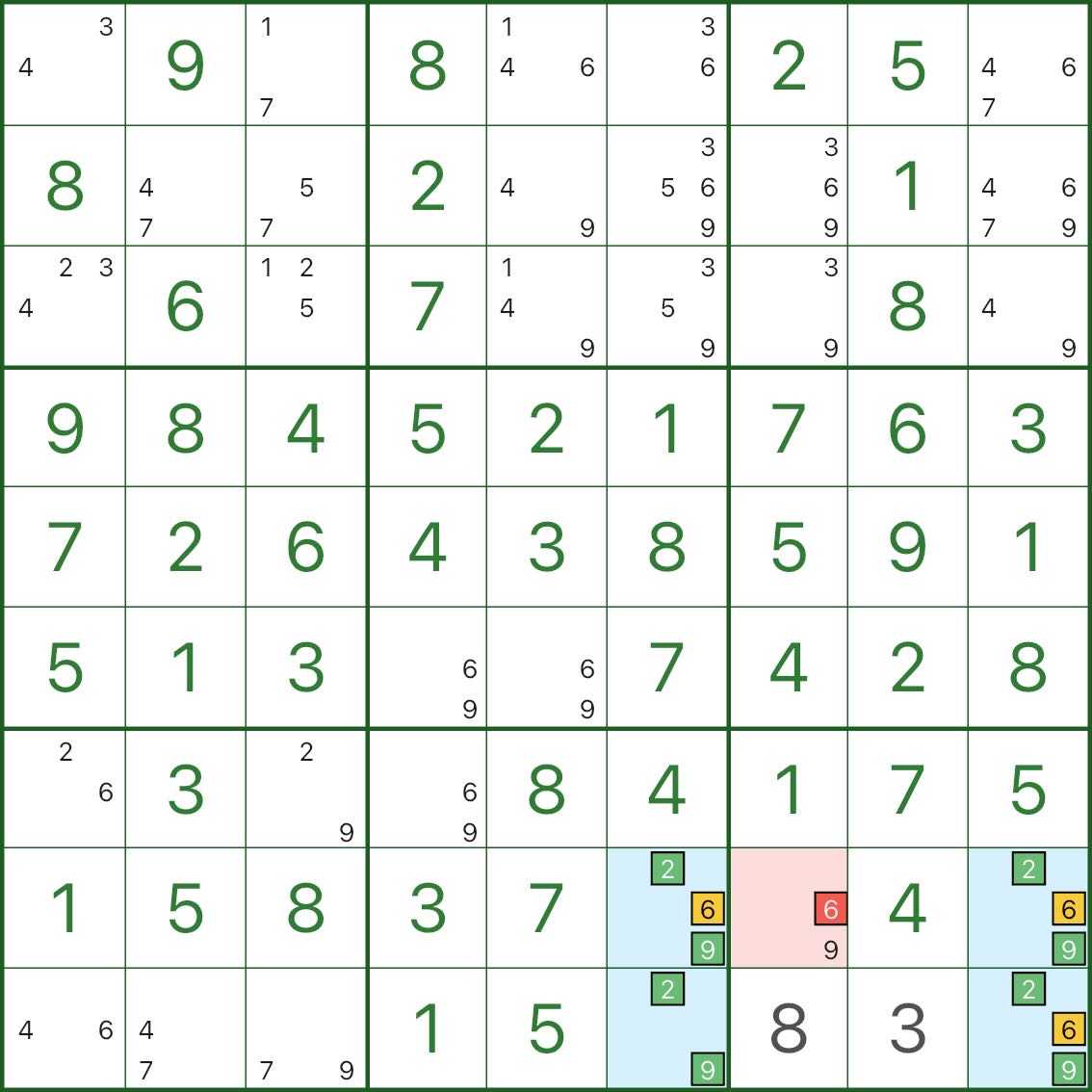
Type V is not strictly “three roofs”. The key idea is:

• there are 2 or 3 roof cells in the rectangle, and they all share the same extra candidate c
• if there are only 2 roof cells, they typically do not share the same row/column/box (if they do, it’s closer to Type II)
• if a cell’s candidate c can see all those roof cells, then that c cannot be true and can be eliminated

In this image, the blue rectangle mainly involves digits 2, 6, 9:

• three blue corners are {2,6,9}
• the remaining blue corner is {2,9} (missing 6)

Now look at the red cell r8c7: it has candidate 6, and it can see all the {2,6,9} roof cells in this pattern.

If r8c7 = 6:

• all three roof cells would be forced not-6
• they would collapse into {2,9} only
• the rectangle becomes a deadly {2,9} pattern (breaking uniqueness)

So the candidate 6 in r8c7 cannot be true and can be eliminated.

---

3. Examples

Images 1–5 in this article are already the examples for Type I–V.
When you practice, try to spot the blue rectangle first, then match the yellow/red marks to the reasoning above.

---

4. How to spot a Unique Rectangle

In real puzzles, you can search in this order:

1. Look for four empty cells that form a 2×2 rectangle (two rows × two columns) and span exactly two boxes
2. Check whether all four corners share the same two core candidates (the “deadly pair”)
3. Then classify by how the extra candidates look:
   • only one corner has extra candidates → Type I (often a forced value)
   • two corners share the same extra digit c → Type II
   • the roofs’ extra digits can form a subset in a row/column/box → Type III
   • in a house, one core digit appears only in two rectangle cells → Type IV
   • two or three corners share the same extra digit c (for 2 roofs, they usually do not share a house) → Type V

That’s UR in one sentence: never allow the rectangle to collapse into a deadly pattern—otherwise uniqueness would be broken.