Swordfish

Tip: Swordfish is basically an “upgraded” X-Wing.
If you haven’t read X-Wing yet, it’s worth starting here:
X-Wing

Swordfish is easier than it sounds. Think of it like this:

Three rows (or three columns) lock the same digit into three columns (or three rows), so that digit can be removed from the rest of those columns (or rows).

We use r1c1 to describe a cell position: r = row, c = column.

---

When can you use it?

Use this 3-step checklist (focus on one digit d):

1. Find three rows (or three columns)
2. In those three rows, all candidates of d are confined to the same 3 columns (they may be fewer, but must not spill into other columns)
3. That forms a small 3×3 net
   ⇒ In those 3 columns, any candidate d outside the net can be eliminated
   (The “three columns lock three rows” version is the same with rows/columns swapped.)

A quick mnemonic: “Three rows lock three columns; outside the net, delete the digit.”

---

A demo example (the first three images are the same example)

Step 1: Spot the “net” (image above)

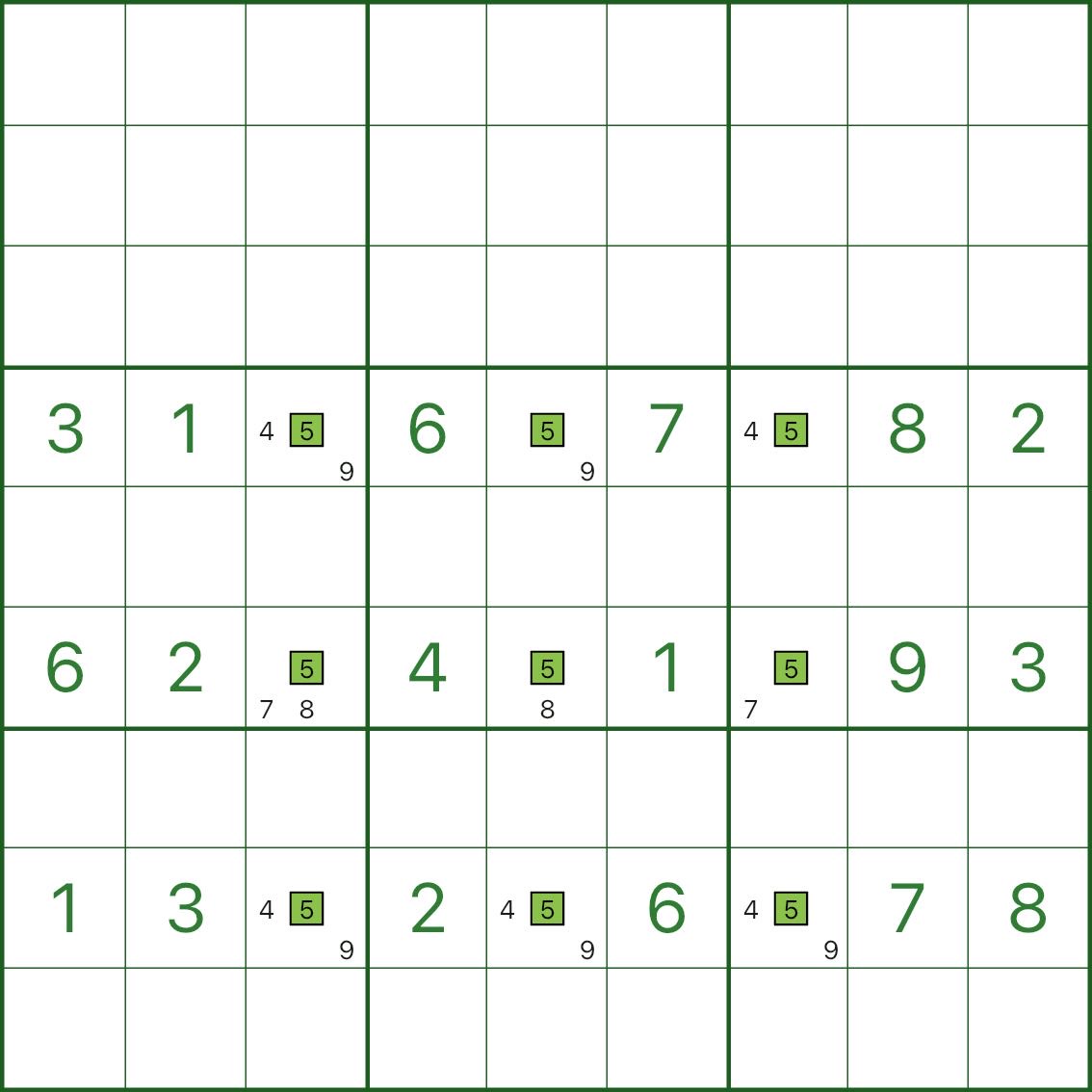
In the image above, we only focus on rows 4, 6, and 8.
The green candidate 5 positions all sit at intersections with columns 3, 5, and 7 — that’s the Swordfish “body” (the net).

Step 2: Use a small “assumption” to build intuition (image below)

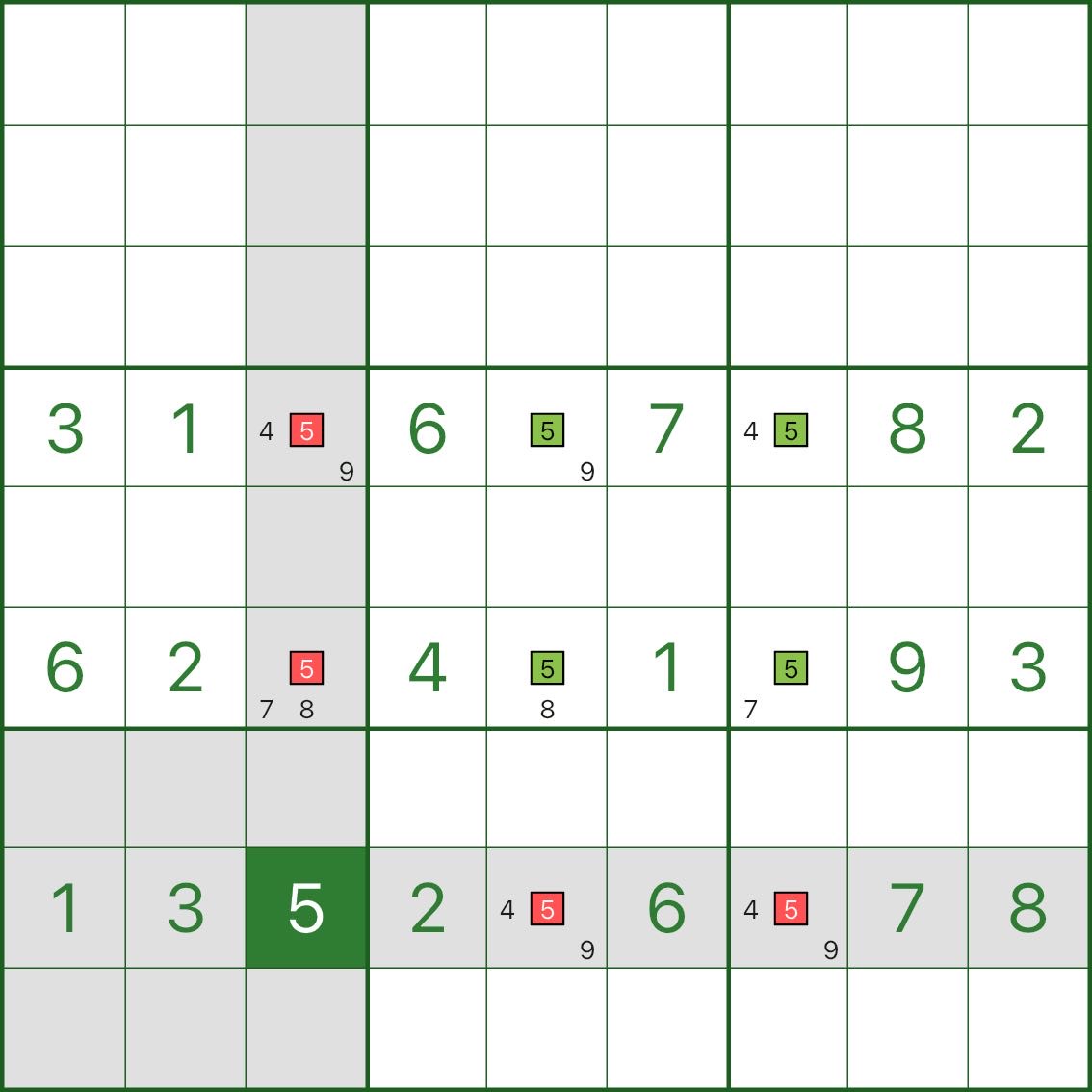
This is not asking you to actually place a number — it’s just to make the idea feel obvious:

• Assume r8c3 = 5
• Then on row 8, no other cell can be 5
• And on column 3, no other cell can be 5
  So the red candidate 5 marks in the image are eliminated.

Step 3: You’ll see it “reduces to X-Wing” (image below)

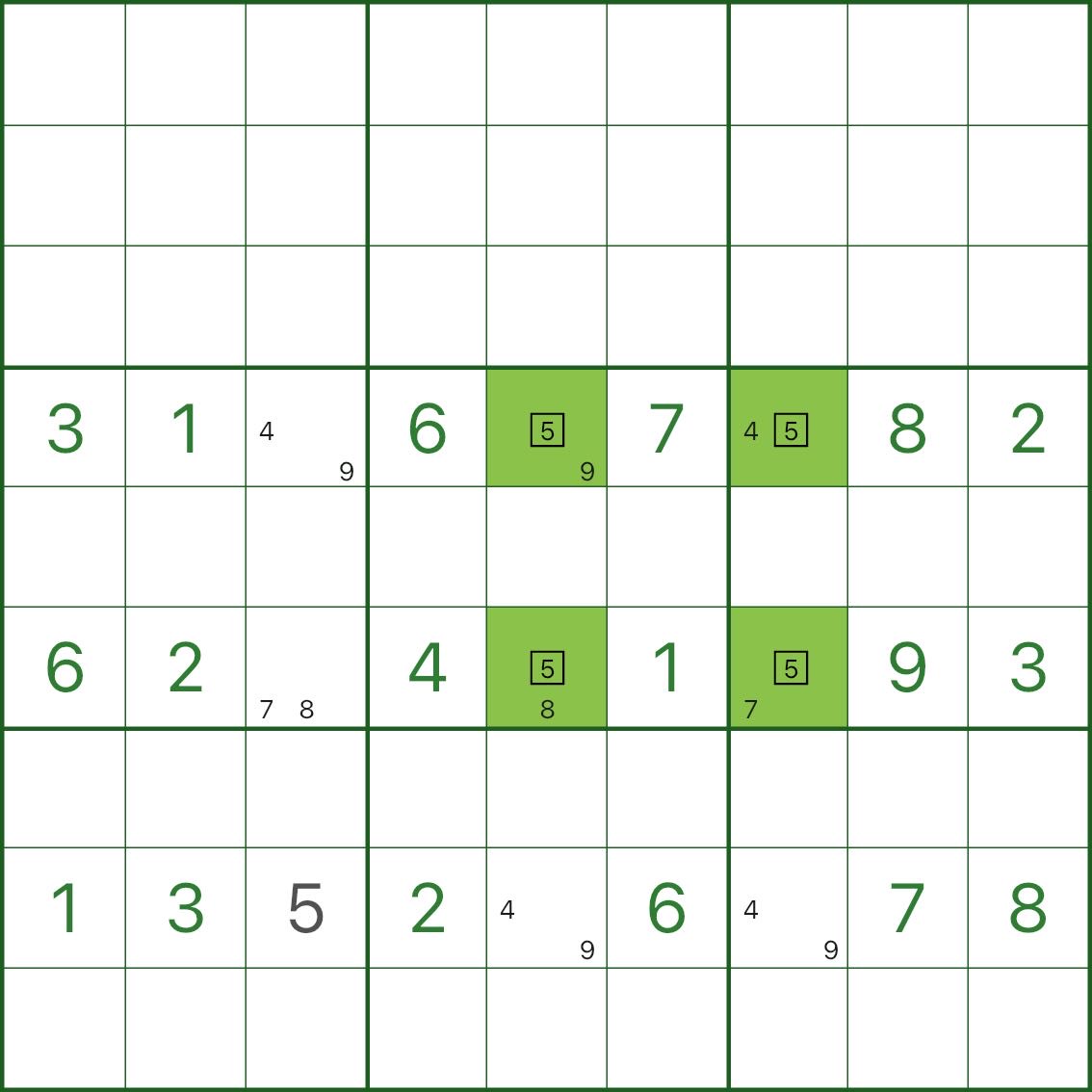
Once row 8’s 5 is “fixed” on a corner of the net, the remaining candidates in rows 4 and 6 become more “aligned”, forming an X-Wing pattern you already know.

That’s the intuition of Swordfish:
no matter which corner row 8 ends up using for digit 5, the net still “occupies” digit 5 in columns 3, 5, and 7.
So any candidate 5 in those columns outside the net can be removed.

---

A real puzzle example (image below)

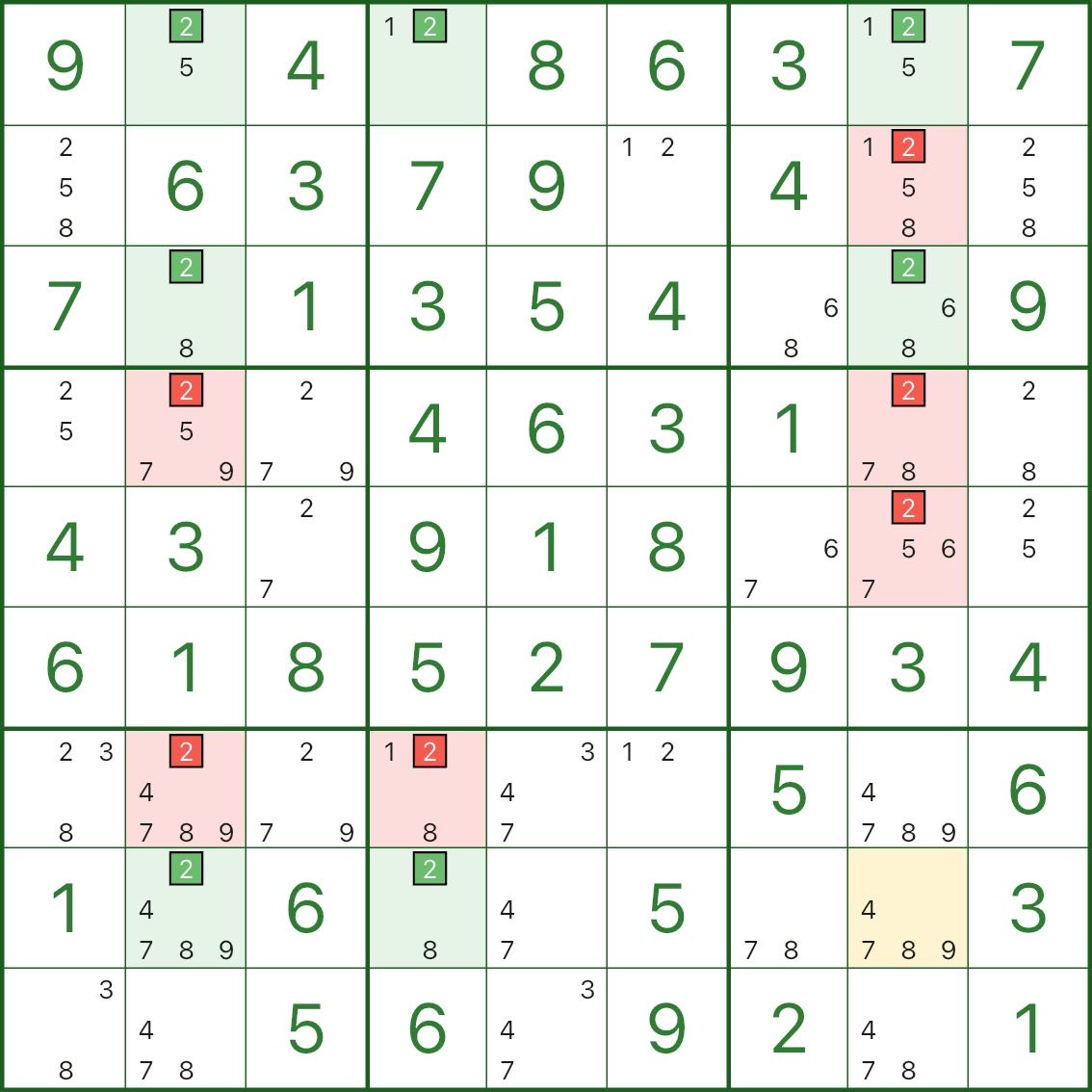
In the image above, rows 1, 3, and 8 form a Swordfish for digit 2, and the body sits within columns 2, 4, and 8.

You might notice:

• r3c4 is already a fixed digit (not a candidate)
• r8c8 doesn’t even have candidate 2

That’s fine. The key condition is:

In those three rows, all candidate positions for digit 2 stay within those three columns.
It can be fewer — but it must not be more.

So in columns 2, 4, and 8, any candidate 2 outside the net is impossible — the red marks show what you can eliminate.

---

Higher-order fish

Once “three rows lock three columns” (Swordfish) makes sense, bigger fish are just larger nets:

• 4th-order fish (Jellyfish): four rows lock four columns (or vice versa)
• 5th-order fish: same idea

The reasoning is identical: the digit is confined to the net intersections, so candidates outside the intersections on the cover lines can be eliminated.
We won’t write separate docs for the higher-order fish here — just reuse the Swordfish thinking.