Grouped Chain

Prerequisite: X-Chain, AIC (Standard Chain)
You’ll see this idea inside: Grouped X-Chain, Grouped AIC

Overview

In normal chains (X-Chain / XY-Chain / AIC), a “node” usually means:

• a single candidate in a single cell (for example, candidate 7 in r1c1), or
• an either-or inside a bivalue cell (a cell with exactly 2 candidates)

A Grouped Chain adds one more kind of node: a candidate group.

The idea is simple: instead of treating each candidate position as a separate point, we sometimes treat “a small set of positions inside the same house” as one combined node.

You don’t need to decide which exact cell is true yet — you only need the group-level fact:

the digit must land somewhere inside this group.

In our UI, a candidate group is shown as a yellow dashed outline (a “group node”).

---

Walkthrough

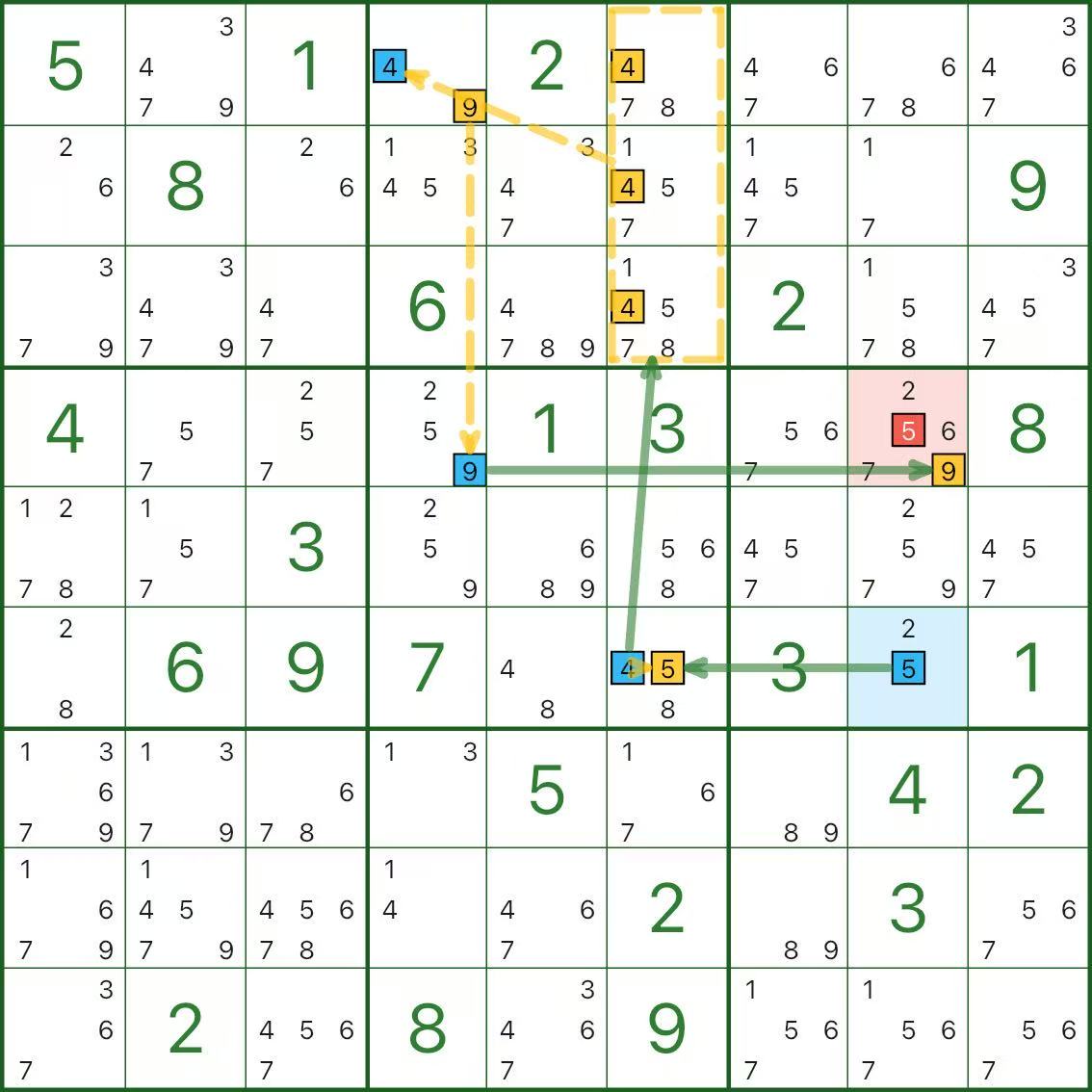
In the image above, focus on the yellow dashed outline inside box 2: r1c6, r2c6, r3c6.

In a normal chain, these would be three separate points. In a grouped chain, we treat them as one candidate-group node:

• If the chain forces “the group is true”, it means: the digit must be placed in one of these three cells (we don’t need to know which one yet).
• If the chain forces “the group is false”, it means: none of these three cells can take that digit.

Why is this valid? Because many steps only need the group’s effect:

• For an outside cell: if it can see the entire group, then
  no matter which cell in the group is true, the same conflict happens.
• For the chain propagation: grouping lets the chain keep an alternating strong/weak structure and continue.

That’s the key difference:
a node can be not only one candidate, but also a group of candidates.

---

Examples

Here are two more grouped-chain examples. Treat the dashed outline as “one big node” first:

---

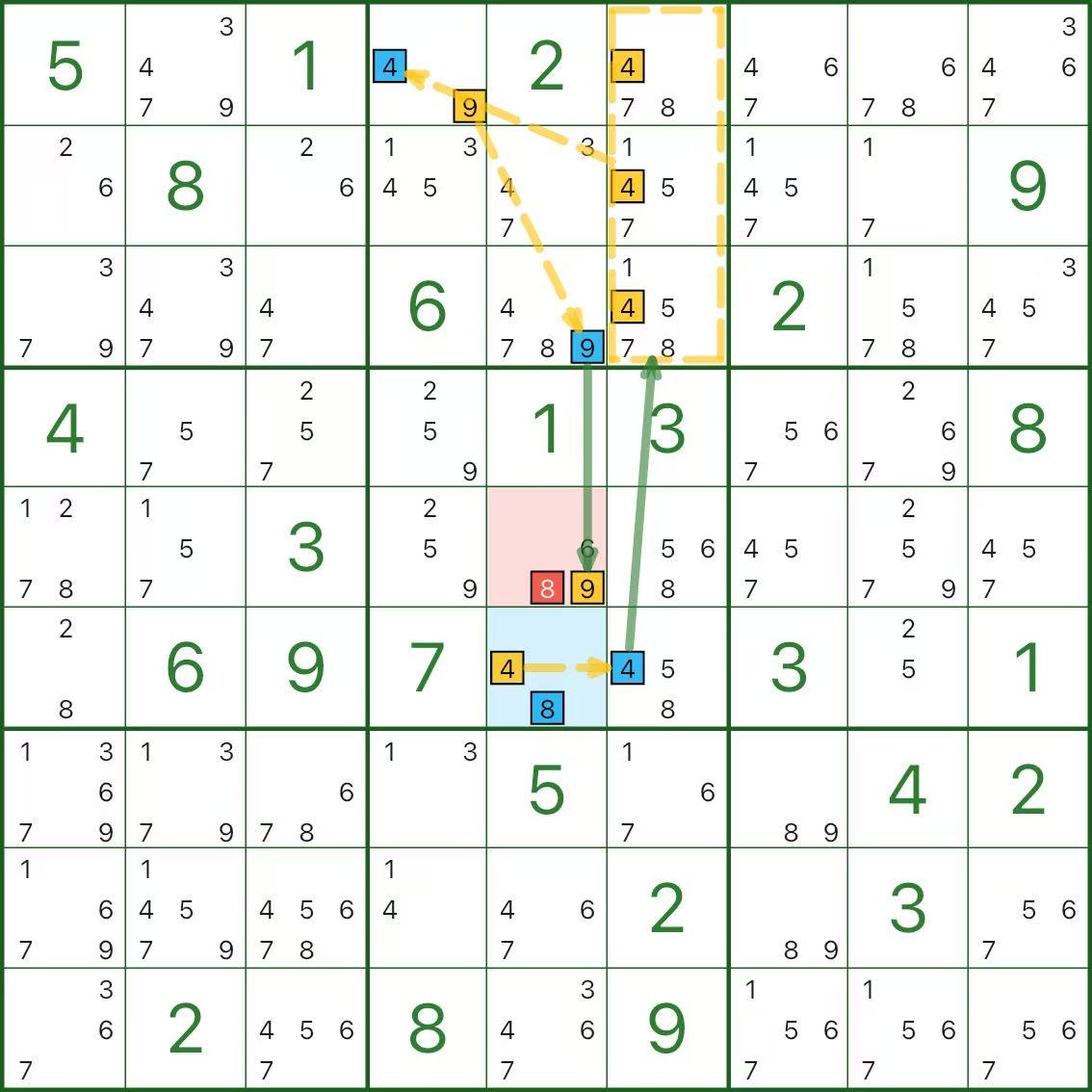
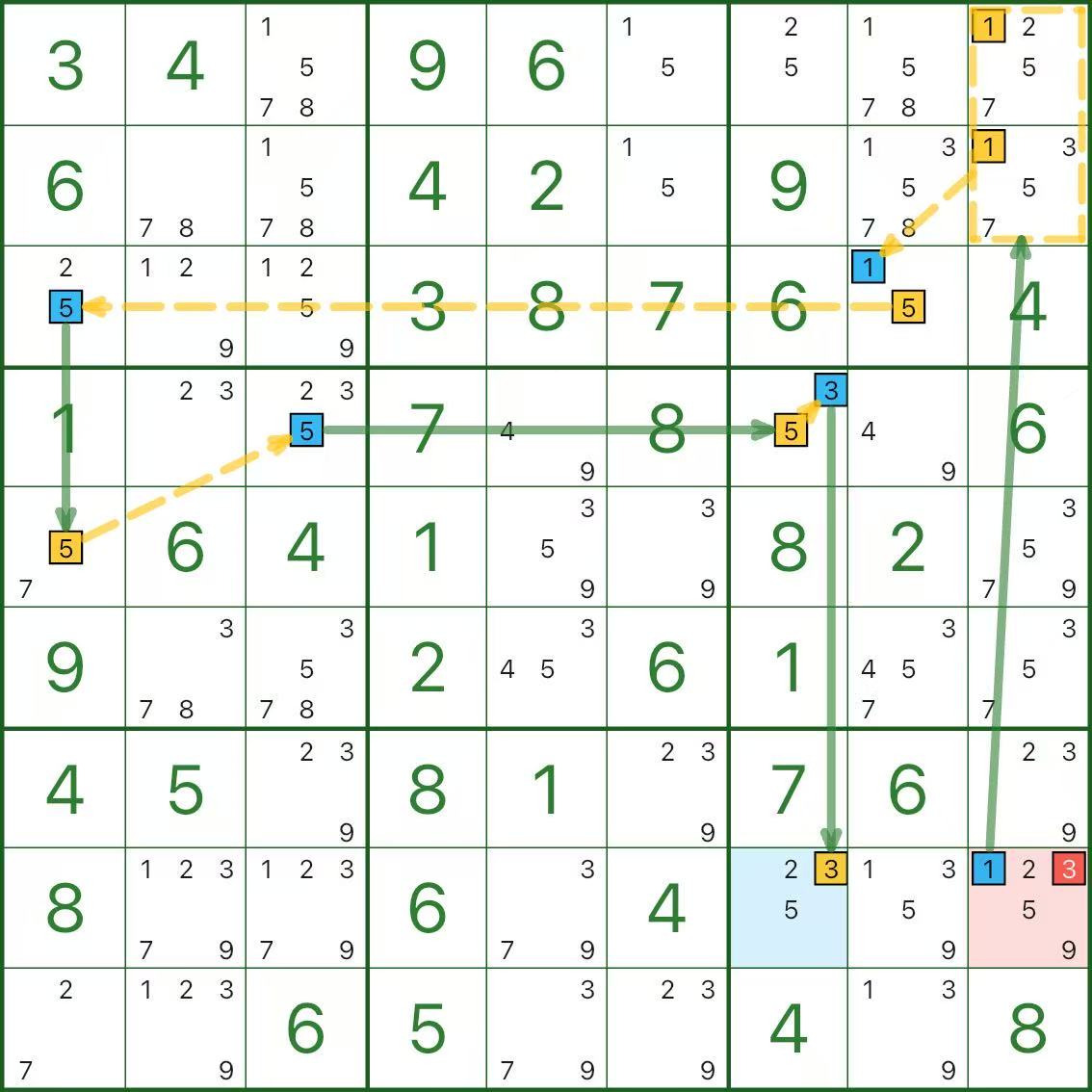
How to Spot a Grouped Chain

One-line checklist: build a normal alternating chain first; if it gets stuck, see whether a small candidate set can be “packed” into a single group node.

In a real puzzle:

1. Start with X-Chain / AIC thinking (strong links + weak links)
2. If a digit has more than two positions in a house but forms a natural small set (shown as a dashed outline), treat it as a candidate group
3. Continue linking while keeping strong/weak alternation
4. Grouped X-Chain / Grouped AIC are simply the original chains plus this “group node” idea