Pairs & Subsets

Naked/Hidden pairs and subsets

Pairs and subsets are some of the most useful “candidate elimination” techniques. They have different names, but they all do the same thing:

In one house (a row / column / box), a small set of cells and a small set of digits “reserve the slots” for each other — so those digits can’t appear elsewhere in that house.

You don’t need to memorize the jargon. A simple rule of thumb:

• Naked: start from what the cells show (these cells contain only these digits)
• Hidden: start from where a digit can go (these digits can only go in these cells)

---

1. Naked Pair

In the same house, if two cells both contain only the same two candidates (for example {a,b}), you have a naked pair.

That means:

• One cell must be a, the other must be b (order unknown)
• So candidates a and b can be removed from every other empty cell in that house

First, look at the image below: focus on the highlighted Box 3 and the two green cells r2c9 and r3c9.
You’ll notice they can only be {1,5}.

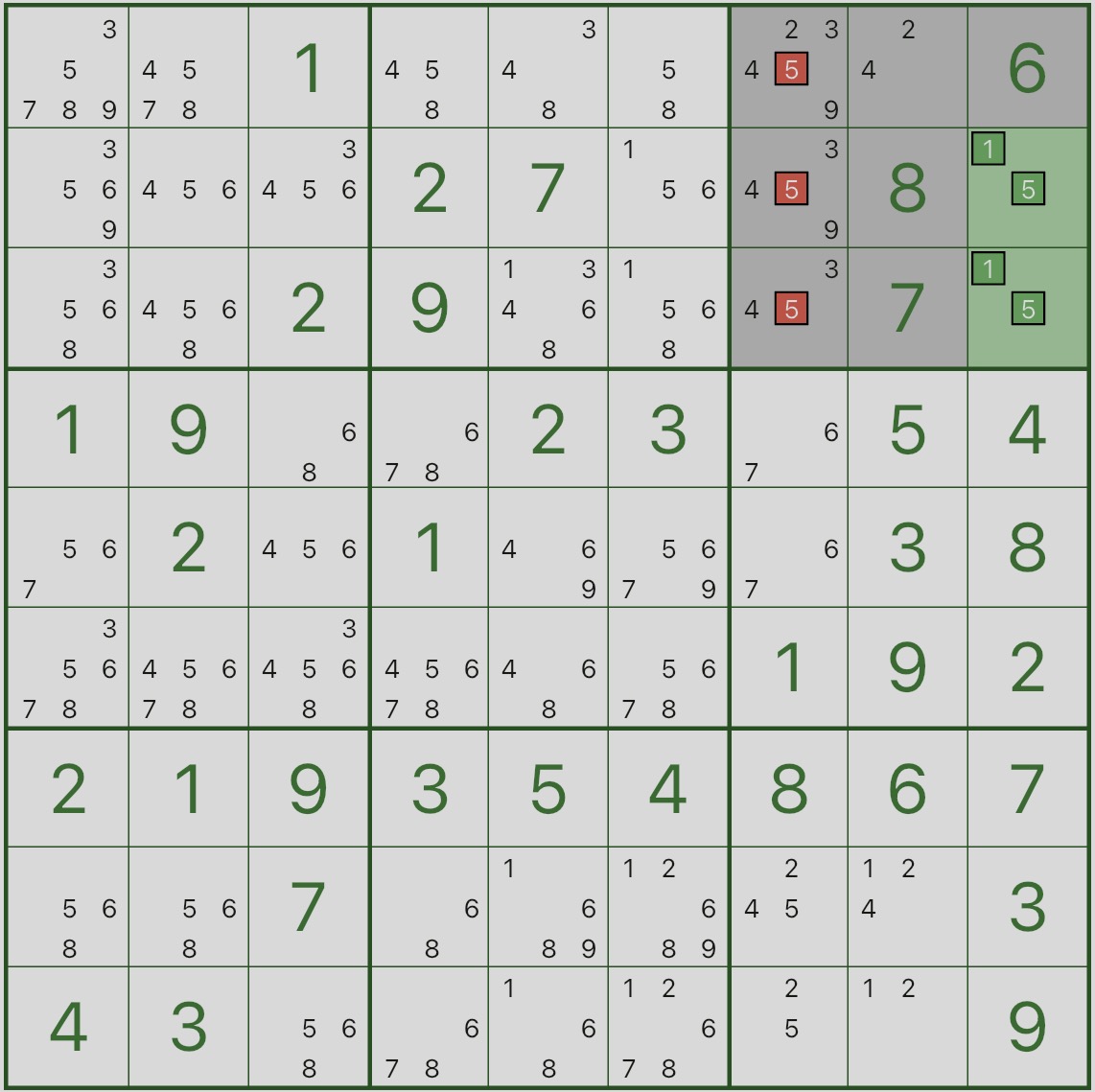
This means: in Box 3, digits 1 and 5 are “reserved” for r2c9 and r3c9.

Now look at the red candidates: the candidate 5 in r1c7, r2c7, r3c7 can be removed.

A quick proof by contradiction:

• Assume r1c7 is 5 (the same logic applies to r2c7 and r3c7)
• Then Box 3 already contains a 5, so r2c9 and r3c9 cannot be 5 and are forced to be 1
• But r2c9 and r3c9 share the same column (column 9), so they can’t both be 1 — contradiction
  ⇒ those red 5 candidates are impossible and can be removed

---

2. Hidden Pair

In the same house, if candidate a appears in exactly two cells, and candidate b also appears in the same two cells, you have a hidden pair.

Those two cells may show extra candidates, but a and b are already locked to them, so you can:

• Remove every candidate except a and b from those two cells

First, look at the image below: focus on the highlighted column 4.
Find where candidates 4 and 5 appear in that column — you’ll see they appear only in r1c4 and r6c4.

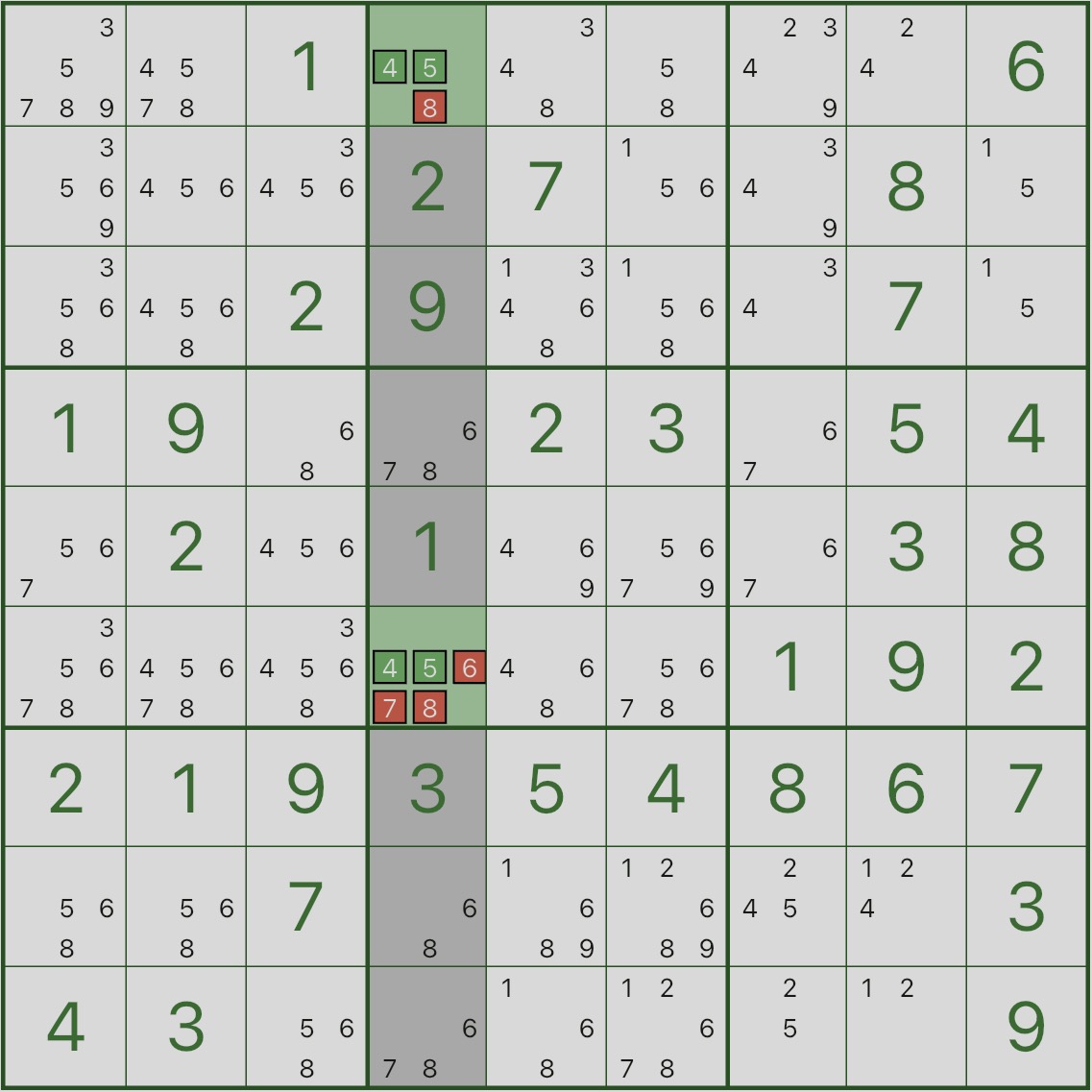
This means: in column 4, digits 4 and 5 must be placed in r1c4 and r6c4.

Why can we remove other candidates from r1c4 and r6c4?

• Assume r1c4 takes a digit that is not 4 or 5
• Then both 4 and 5 would have to fit into r6c4 only
• A single cell can’t be both 4 and 5 — contradiction
  ⇒ r1c4 and r6c4 must be {4,5}, so other candidates in those cells can be removed

---

3. Naked Subset (Triple / Quad)

This is the “naked pair” idea, generalized:

If N cells in a house collectively contain only N digits (for example three cells contain only {a,b,c}), you have a naked triple. The same idea applies to quads.

Those digits must be placed within those N cells, so:

• Remove those digits (for example a, b, c) from every other empty cell in that house

First, look at the image below: focus on the highlighted row 8 and the three cells r8c1, r8c2, r8c4.
You’ll notice these three cells collectively contain only {5,6,8}.

This means: in row 8, digits 5, 6, 8 must be placed within r8c1, r8c2, r8c4.

That’s why the red 5, 6, 8 candidates in the rest of row 8 can be removed.

A simple contradiction view:

• If another cell in row 8 “takes” one of {5,6,8}
• Then those three cells would have to be filled using only two digits for three cells
• That can’t work — contradiction

---

4. Hidden Subset (Triple / Quad)

This is the “hidden pair” idea, generalized:

If N digits in a house appear only in the same N cells (even if those cells contain extra candidates), you have a hidden triple/quad.

Those N digits are locked to those N cells, so:

• Remove every candidate except those N digits from those cells

First, look at the image below: focus on the highlighted column 5.
You’ll notice digits 4,7,8 appear only in r1c5, r8c5, r9c5.

This means: in column 5, digits 4, 7, 8 must be placed within r1c5, r8c5, r9c5.

Therefore, in these three cells we can remove any other candidates that are not 4, 7, or 8.

Why is that safe?

• If any of these cells took a different digit
• Then 4, 7, and 8 would have fewer than three spots to fit — contradiction

---

5. Tips to spot them faster

• Keep candidates reasonably complete (you’ll need them for harder puzzles)
• Scan for naked patterns first: start from cells with very few candidates (2, 3, or 4)
• Then scan for hidden patterns: in a house, check if a digit is limited to 2, 3, or 4 spots
• After eliminations, pause and look again — simplified candidates often reveal the next step