Empty Rectangle

Prerequisite: Chain Basics

Description

Empty Rectangle is a single-digit candidate elimination technique: focus on one digit d.

Inside a box, digit d may form a special cross / L-shaped distribution — meaning all d candidates in that box lie on one row and one column.
If a short chain forces d onto those lines, you can sometimes reach a very clear contradiction: the box ends up with no place for d, so the original assumption must be wrong.

---

Explanation

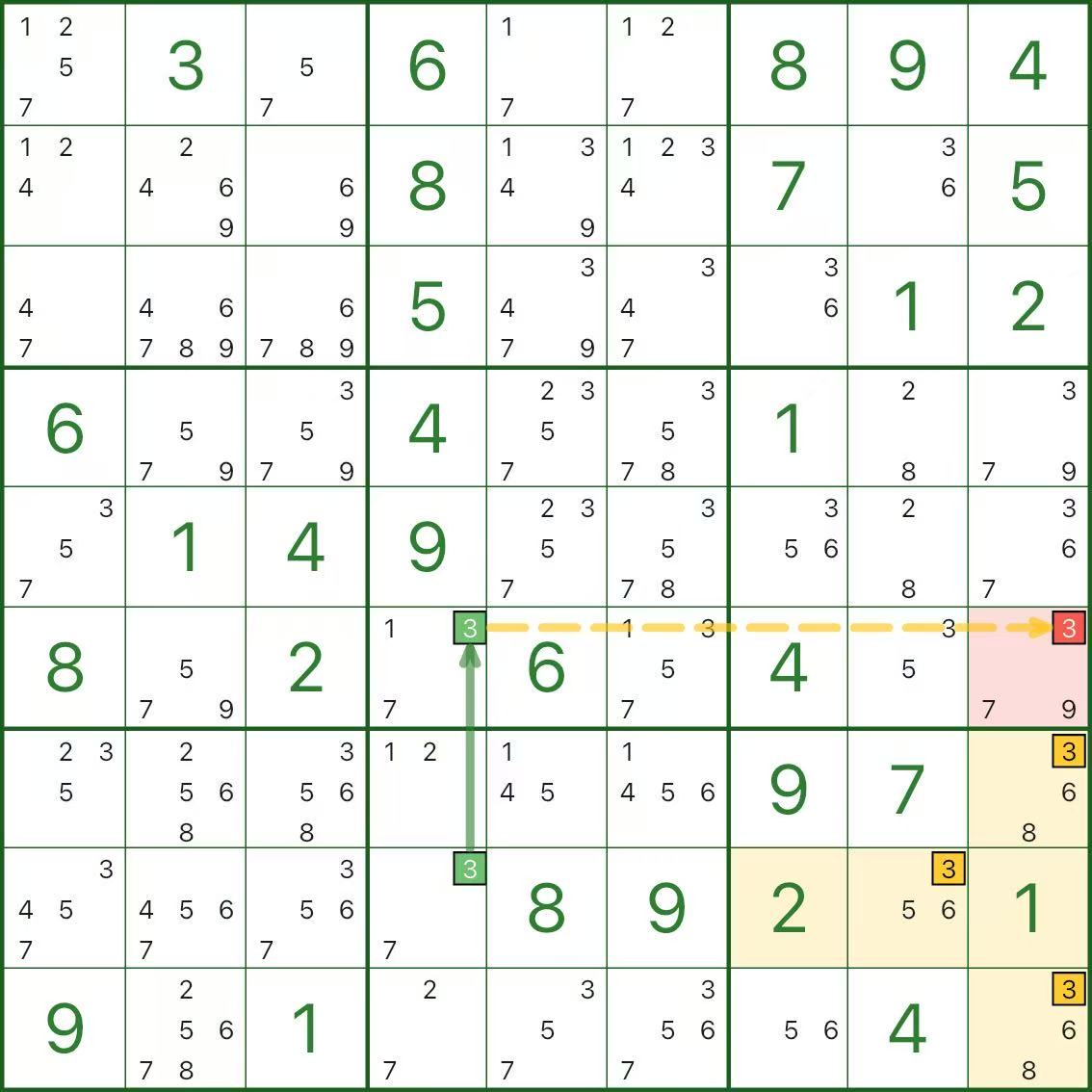
In the image above, we want to eliminate candidate 3 in r6c9 (red).

Here is the short contradiction:

• Assume r6c9 = 3 (the red candidate is true)
• A row cannot contain two 3s, so r6c4 ≠ 3
• In column 4, digit 3 has only two possible cells: r6c4 or r8c4
  Since r6c4 is not 3, r8c4 must be 3
• Now look at box 9 (the empty rectangle box):
  with r6c9 = 3 (same column) and r8c4 = 3 (same row), all remaining 3 positions in box 9 are eliminated, so box 9 has no place for digit 3 (contradiction)

So the assumption is impossible: r6c9 cannot be 3, and candidate 3 can be eliminated.

---

Examples

These images show more empty rectangle patterns. Use them as references for “box cross/L shape + short chain + elimination (red)”:

---

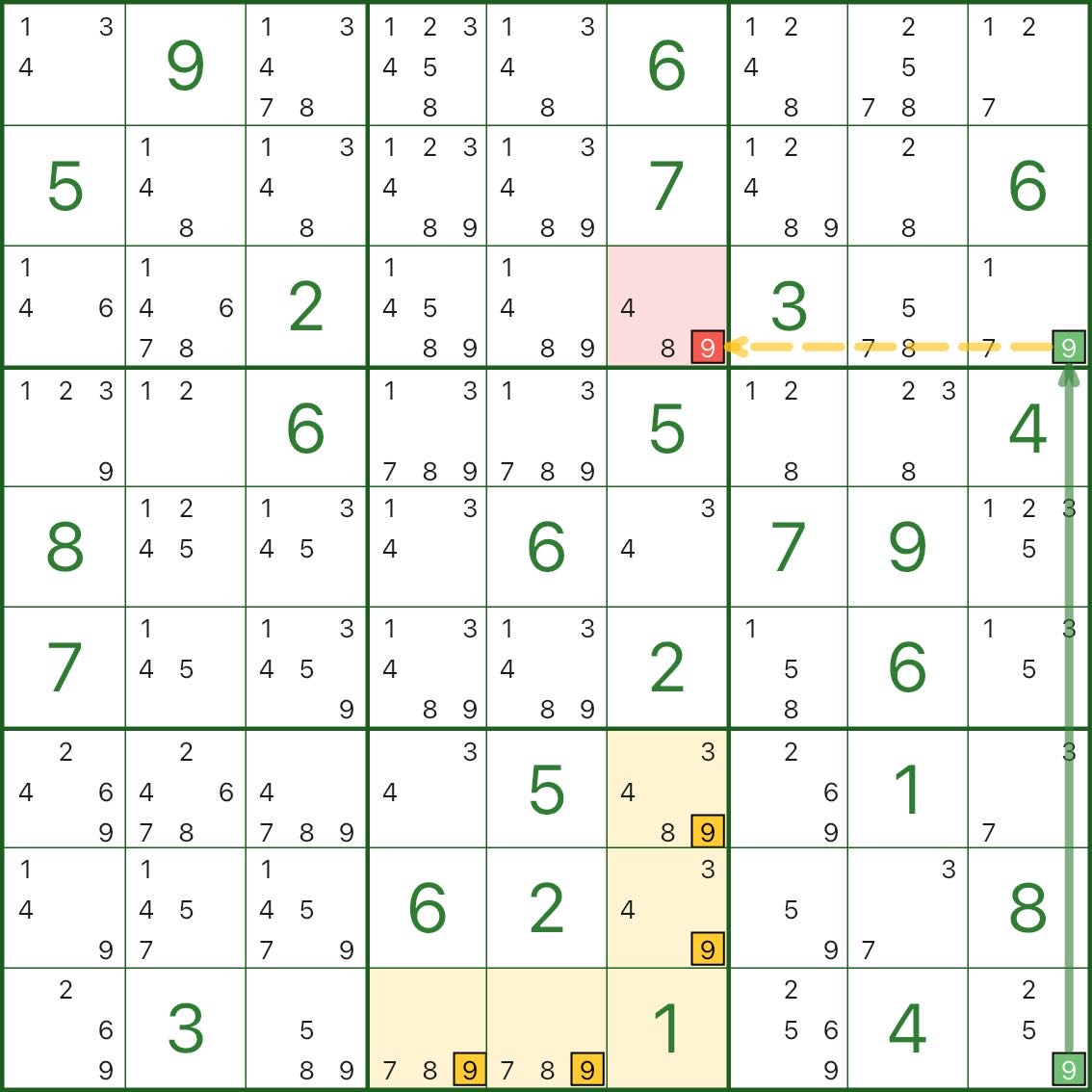
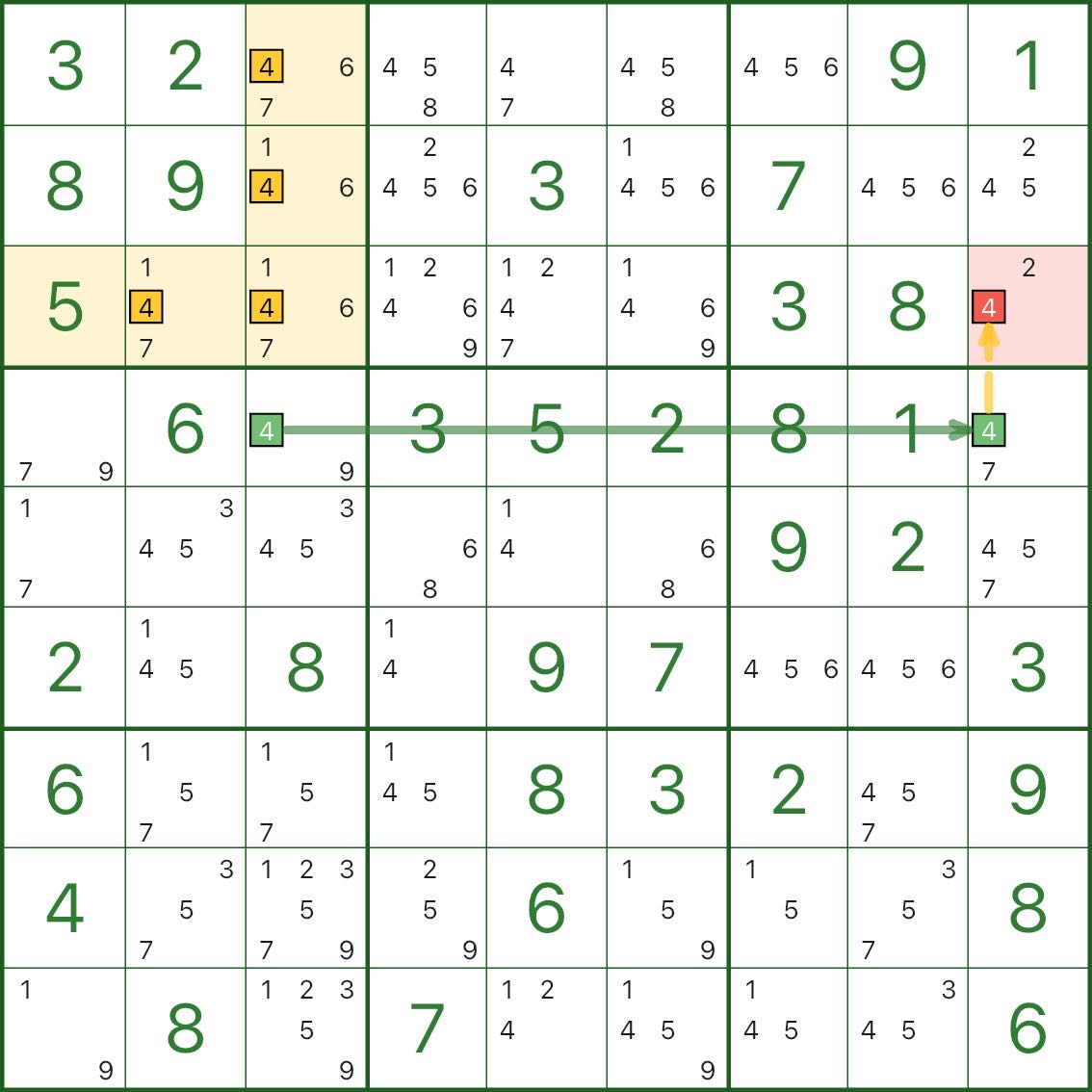
How to Find Empty Rectangle

One-line checklist: find a box where d candidates form a cross/L shape, then use a short chain that would make the box run out of places for d, and eliminate the red candidate by contradiction.

In a real puzzle:

1. Pick a digit d
2. In a box, check whether all d candidates lie on one row + one column (cross/L shape)
3. Look for a short chain so that assuming a red candidate is true forces d onto those lines
4. If that assumption leaves the box with no place for d, eliminate the red candidate d