Chain Basics

Strong links / weak links / alternation (AIC)

Chains are a core building block for many advanced Sudoku techniques.
At heart, a chain is just a sequence of “if…then…” implications that lets deductions travel across the grid.

After this chapter, advanced hints like single-digit chains, kite, skyscraper, medusa, and AIC will feel much more readable.

We use r1c1 to refer to a cell position:
r = row, c = column.

To make the diagrams easier to follow, we use:

• Green solid line: strong link
• Yellow dashed line: weak link
• Blue/Yellow candidate background: two mutually exclusive “states”, to visualize alternation
• Red candidate: the candidate to eliminate in this step

Reminder: a chain is bidirectional. Arrows are only for readability.

---

What is a chain?

In short, a chain connects candidate relations so you can keep applying “if…then…” logic:

If A is not possible, then B must be true;
if B is true, then C must be false;
…

A chain is made of:

• Nodes: candidates (a digit candidate in a cell)
• Links: relations between candidates (strong / weak)

A chain doesn’t necessarily mean “we always delete the start”. It’s more like a reasoning path:

• Reach a contradiction ⇒ prove a candidate cannot be true → eliminate it
• Reach a forced truth ⇒ prove a candidate must be true → place a value

This article focuses on the most common “single-digit chains”: reasoning about candidates of one digit d.
(Bivalue-cell relations and grouped/region strong links are covered later.)

---

Strong links and weak links

Strong link (conjugate pair)

Mnemonic: either-or.

In the same unit (row / column / box), if a digit d appears in exactly two candidate cells, those two candidates form a strong link (a conjugate pair).

The key implication is “NOT forces YES”:

• If NOT A, then B (If A is not d, then B must be d)
• If NOT B, then A

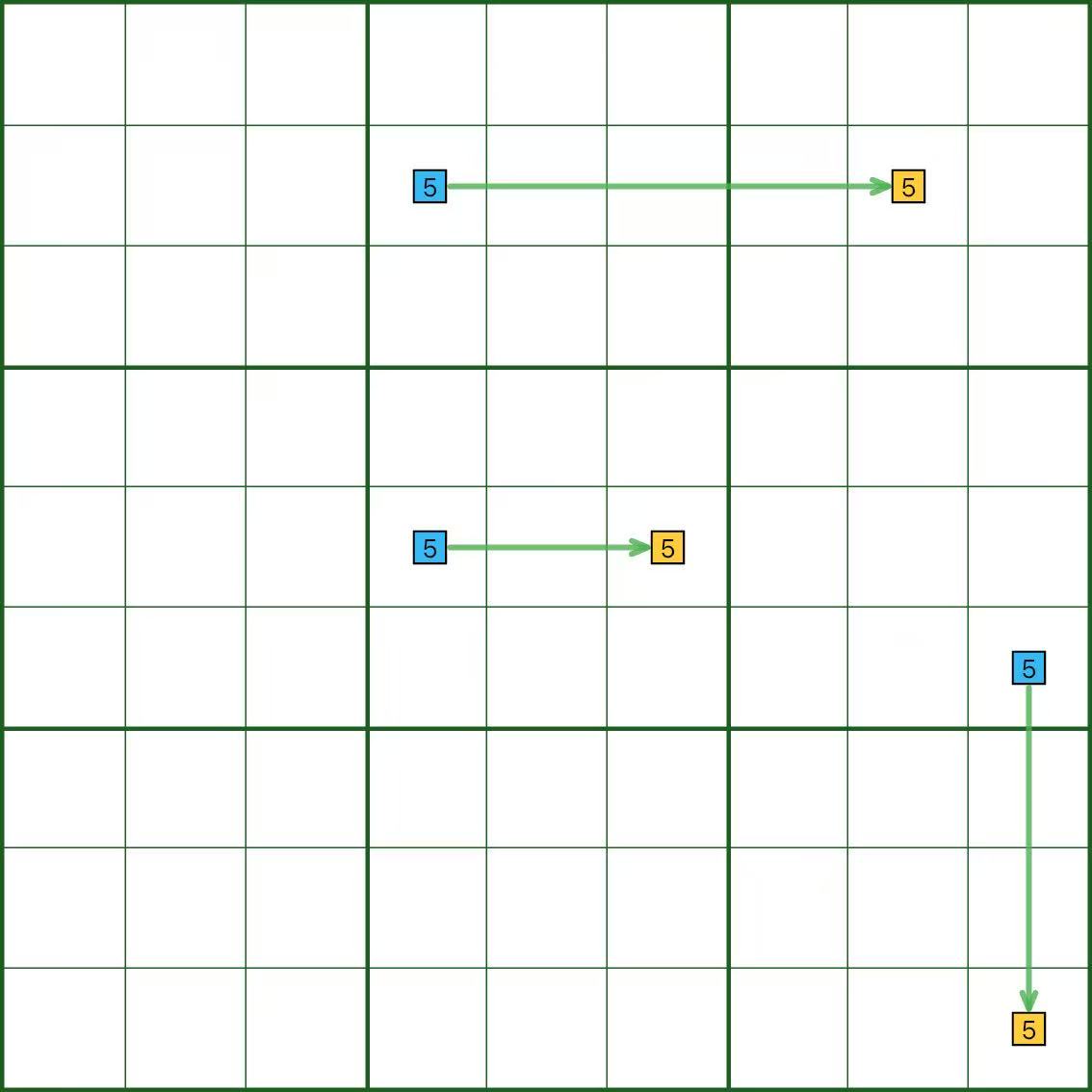
In the diagram, digit 5 forms strong links in a row, a column, and a box.
You can read it from either end; arrows are just a reading aid.

Important note: every strong link is also a weak link.
Since the two candidates share the same unit, they cannot both be true:

• If A, then NOT B (If A is d, then B is not d)

One-line summary:

Strong link = weak exclusivity + “one of them must be true”

Weak link

Mnemonic: if you see each other, you can’t both be true.

A weak link expresses one thing:

Two candidates cannot both be true.

In single-digit chains, the most common weak link is two candidates of the same digit d in the same unit.

Implication:

• If A, then NOT B

But not the reverse:

• If A is false, you can’t conclude B (there may be a third spot).

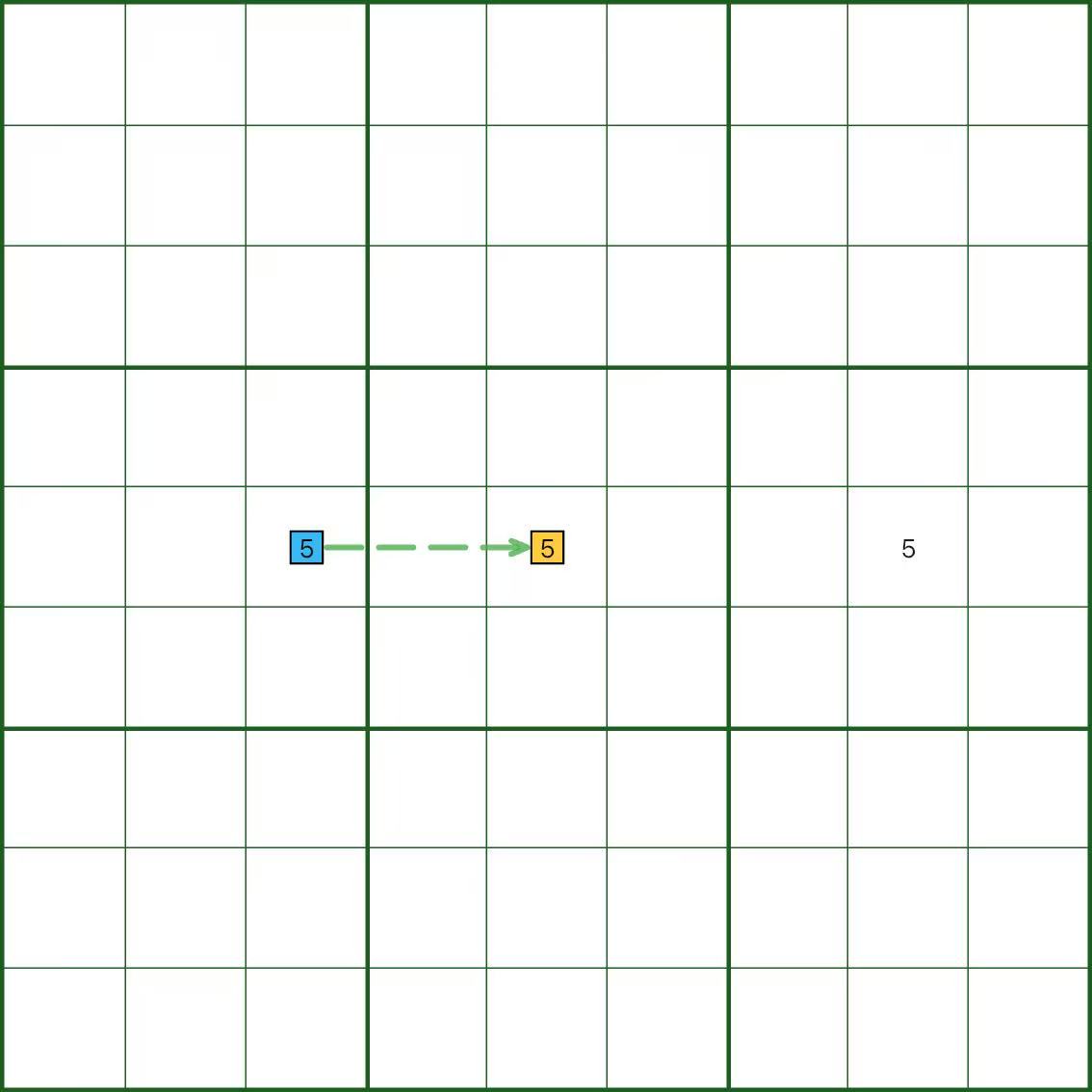
In the diagram, digit 5 has three candidate cells in a row, so every pair is weakly linked.
The picture draws only one dashed segment just to show what a weak link looks like.

---

How do chains work?

To propagate along a chain, remember two rules:

1. True → (weak) → False
   Weak links are exclusive: if A is true, B must be false.

2. False → (strong) → True
   Strong links are either-or: if A is false, the other candidate must be true.

So a working chain typically alternates:

False —(strong)→ True —(weak)→ False —(strong)→ True —(weak)→ False …

Why alternate?

• weak-weak breaks: “false” doesn’t propagate through a weak link
• strong-strong can connect, but in many puzzles it often corresponds to simpler patterns, so chains are most useful for alternating propagation

---

Example

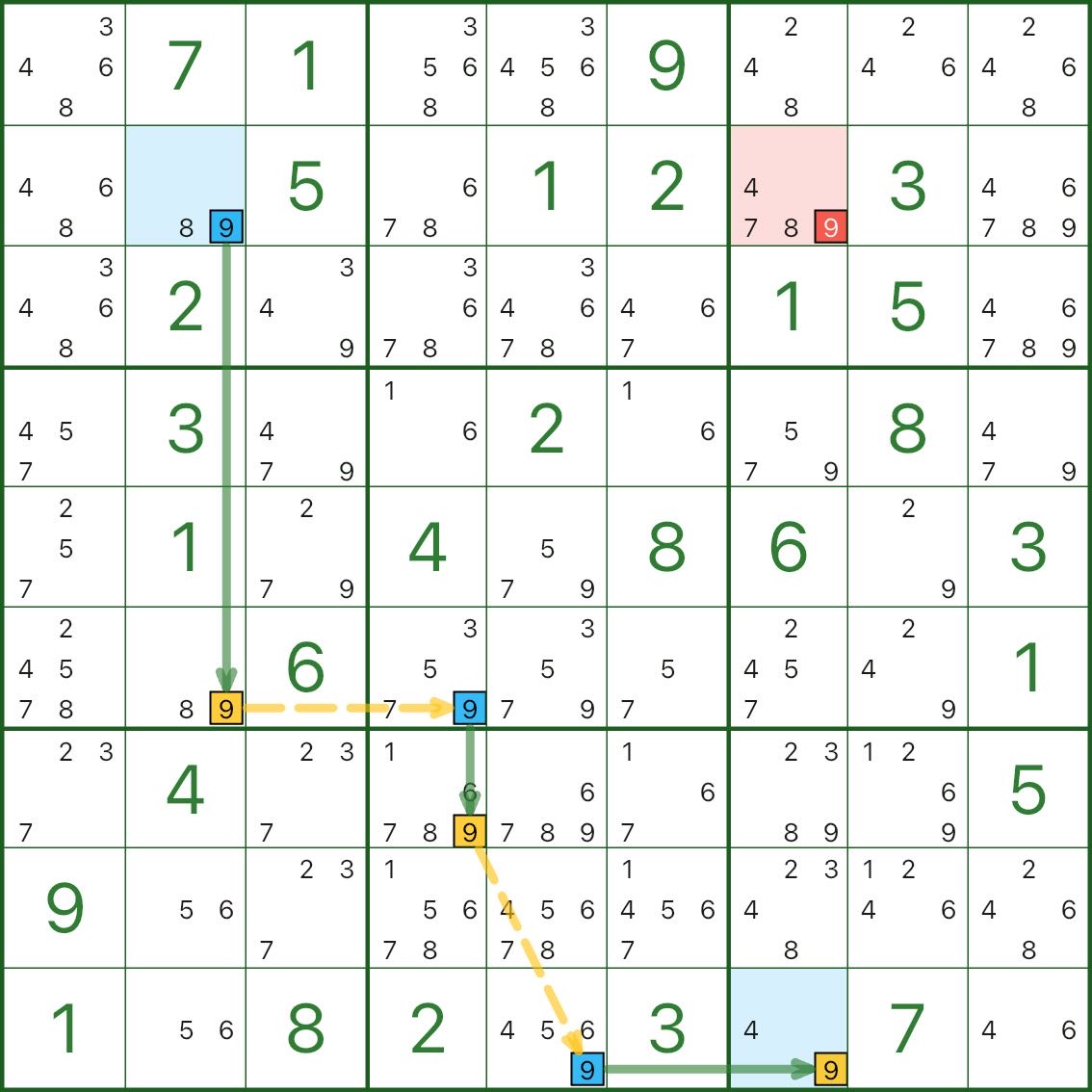
In the diagram, the red candidate is digit 9 in r2c7.

Read it like this:

1. From the highlighted start: once r2c2 is NOT 9, the chain propagates to force r9c7 = 9
   (you can see the clean alternation False → True → False → True → False → True)

2. Now use a contradiction: assume the red candidate r2c7 = 9 is true

   • r2c7 sees r2c2 in the same row, so r2c2 cannot be 9 (r2c2(9) is false)
   • propagate that “false” through the chain, forcing r9c7(9) to be true
   • r2c7 and r9c7 are in the same column, so they cannot both be 9 → contradiction

Therefore, r2c7 cannot be 9, and that red candidate can be eliminated.

---

Practice

The following three diagrams are all single-digit chains. Take your time.

Three quick self-check questions:

1. Which segments are strong links, and why are they “either-or”?
2. Which segments are weak links, and why are they mutually exclusive?
3. Why does the red candidate lead to a contradiction?

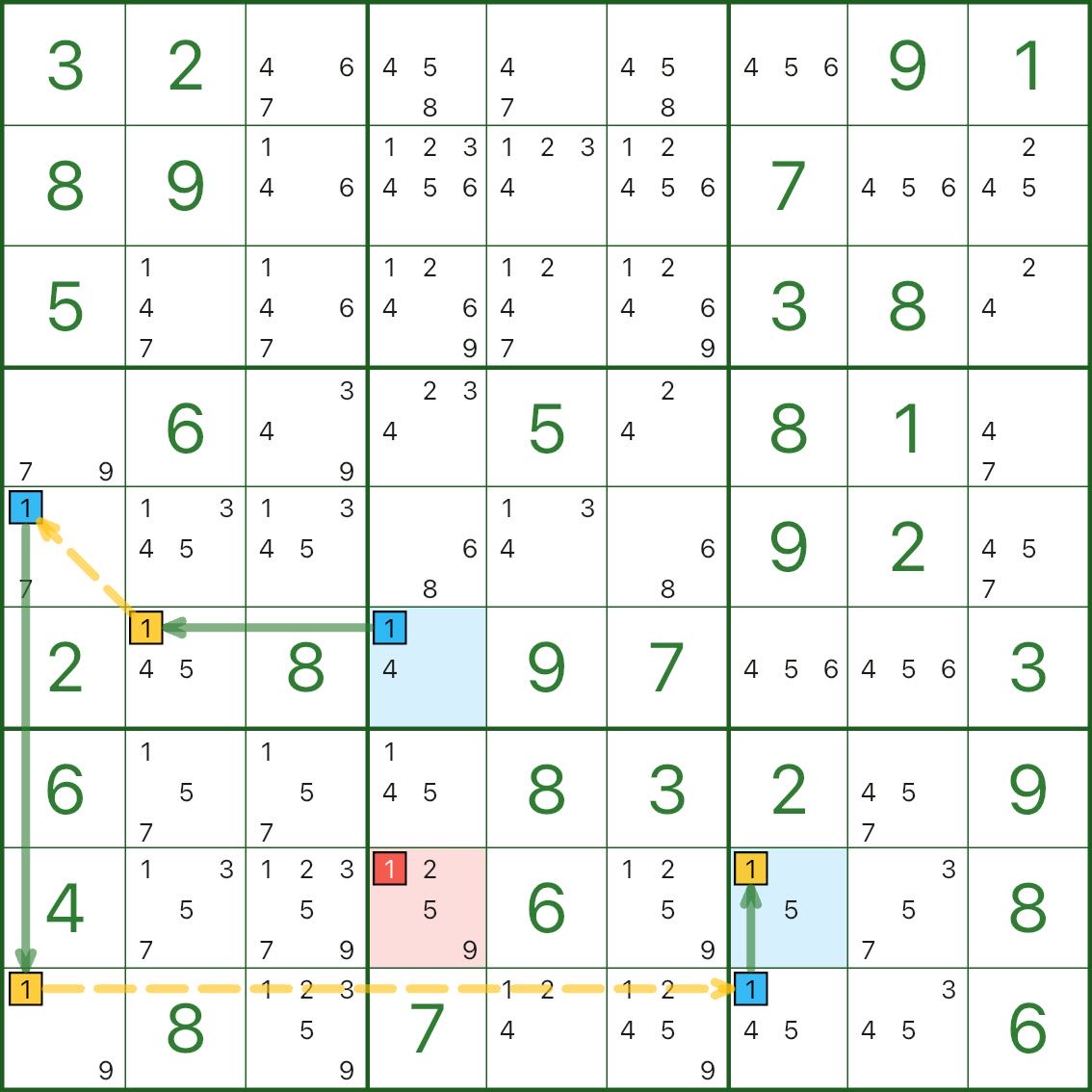
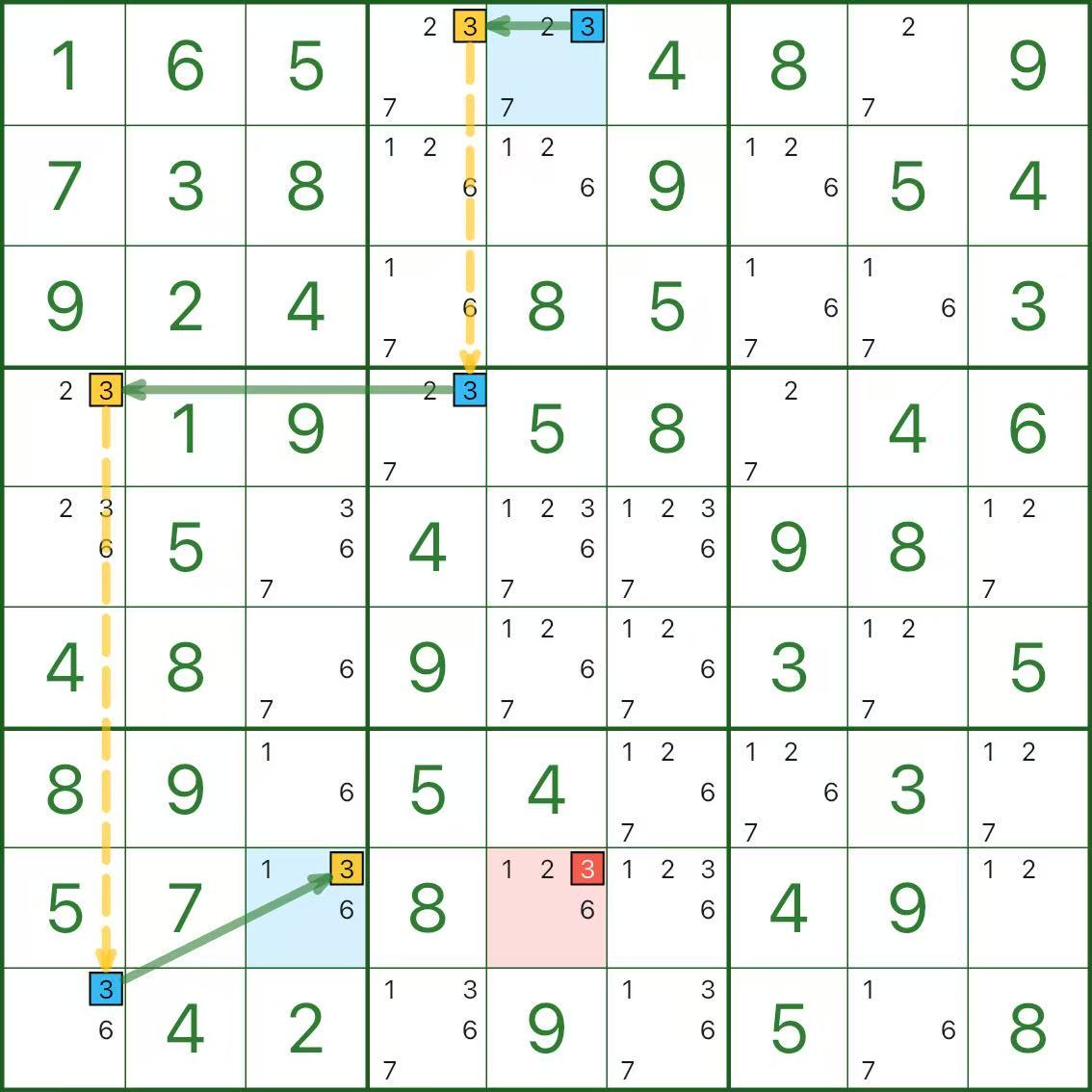
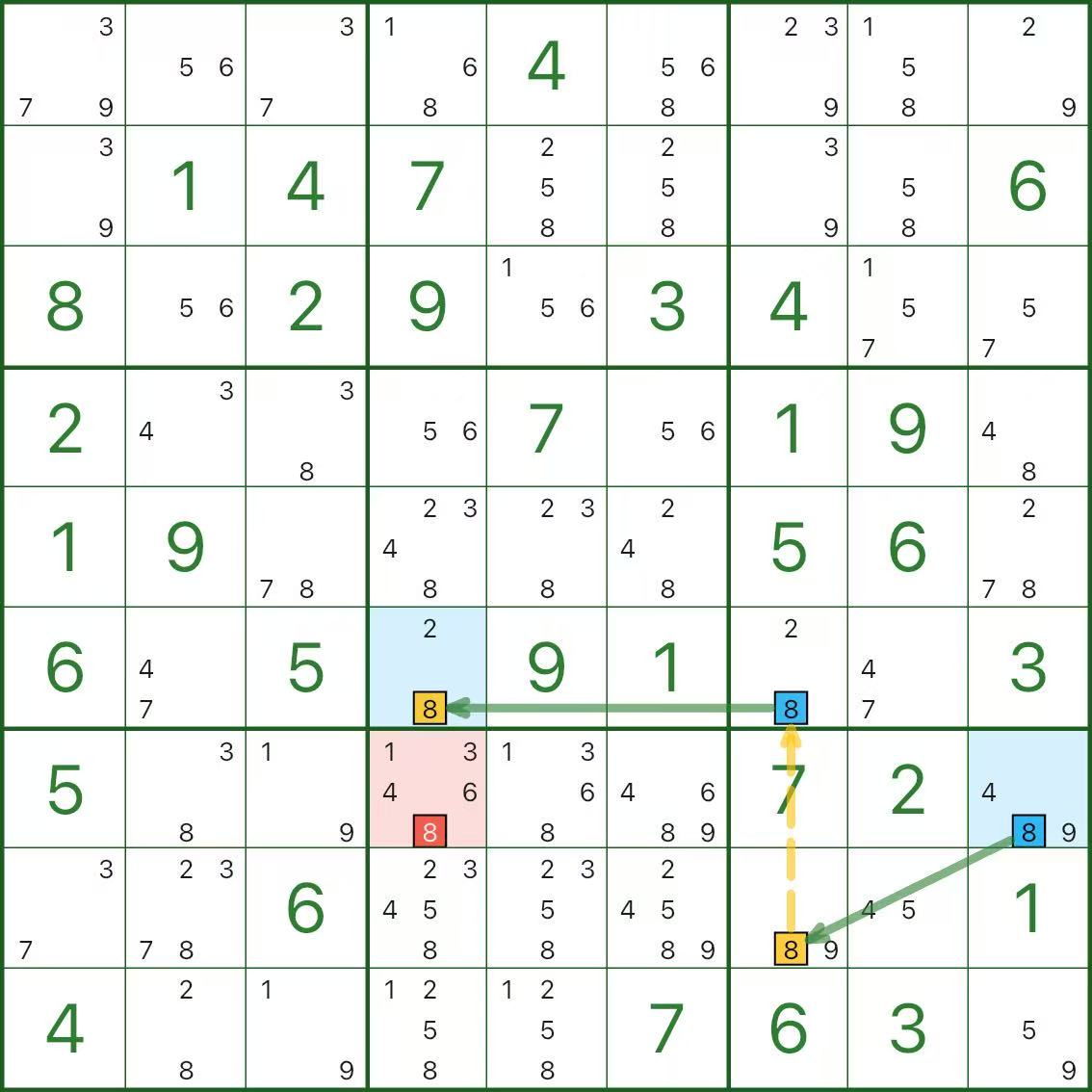
If it feels a bit twisty at first, that’s completely normal.
That’s a chain: the foundation of many advanced techniques—get comfortable with it before moving on.