BUG+1

Prerequisite: BUG+1 relies on the puzzle having exactly one solution.
If you haven’t read it yet, start here:
Uniqueness

---

1. Overview

BUG+1 is short for BUG + 1 — you may also hear it called Bivalue Universal Grave + 1.

The name sounds scary, but it describes a very specific board state:

• almost every unsolved cell is bivalue (exactly 2 candidates)
• one “exception cell” has 3 candidates (that’s the “+1”)

What is BUG?

BUG = Bivalue Universal Grave.

It’s called a “grave” because the grid can feel “stuck”: candidates come in pairs everywhere, and progress often stalls without uniqueness.

When the grid satisfies these two conditions, it becomes a very symmetric “BUG” structure:

1. every unsolved cell is bivalue
2. for any digit d, in every house (row/column/box), the number of candidate positions for d is even
   • most commonly 2
   • if d is already placed in that house, it can be 0 (still even)

This symmetry often allows two valid completions (multiple solutions).

So what is BUG+1?

BUG+1 is “almost a BUG, but not quite”:

• all unsolved cells are bivalue
  except one cell with 3 candidates

That extra candidate breaks the even symmetry — and that’s exactly what lets us force a placement using uniqueness.

So the exception cell has one forced candidate — we can place the digit directly.

---

2. Walkthrough

Step 1: spot the “almost all bivalue” state (top image)

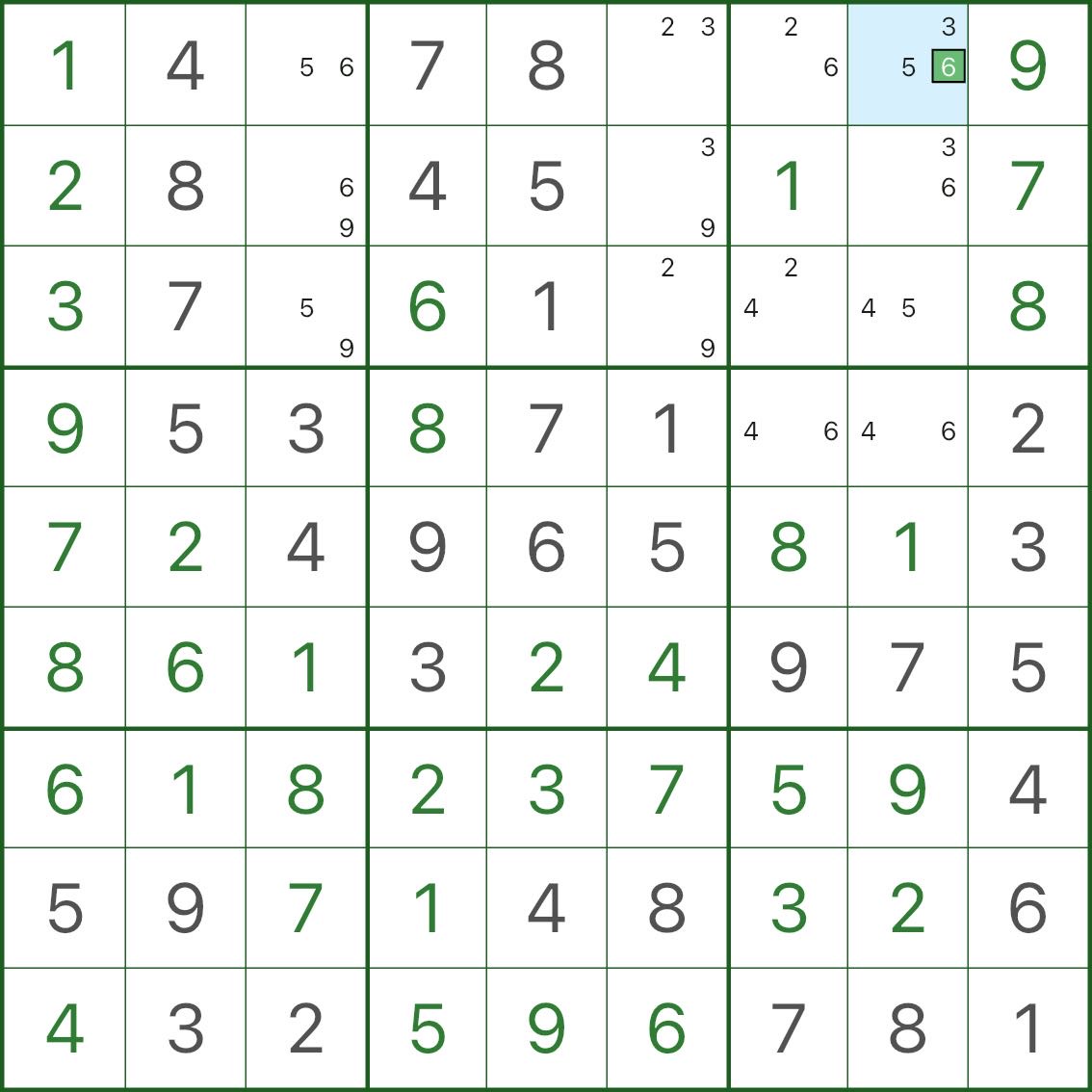
In the image:

• most empty cells show only 2 small candidates
• one cell is the exception, showing 3 candidates (the “+1”)

Step 2: which digit should we place? (and why?)

We only focus on the three candidates in the exception cell, and we do one simple thing: check odd vs even.

How:

1. look at the three candidates in the exception cell
2. for each of those digits, count how many times it appears as a candidate in the exception cell’s row / column / box

You will typically find that one digit appears 3 times (odd) in one of those houses.
That “odd” candidate is the digit you should place.

Why? Use a contradiction:

Assume we do not place this “odd” candidate, and instead pick one of the other two “even” candidates:

1. the exception cell becomes bivalue
2. the candidate distribution across houses returns to an “even” symmetry (a BUG structure)
3. BUG structures often allow two valid completions (multiple solutions)

But the puzzle must be unique, so that choice is impossible.
Therefore the “odd” candidate must be true — that is the digit you place.

If you don’t want to count anything: the hint will highlight the forced candidate for you.

---

3. Example

The image below shows the result: the forced “+1” candidate in the exception cell is placed.

---

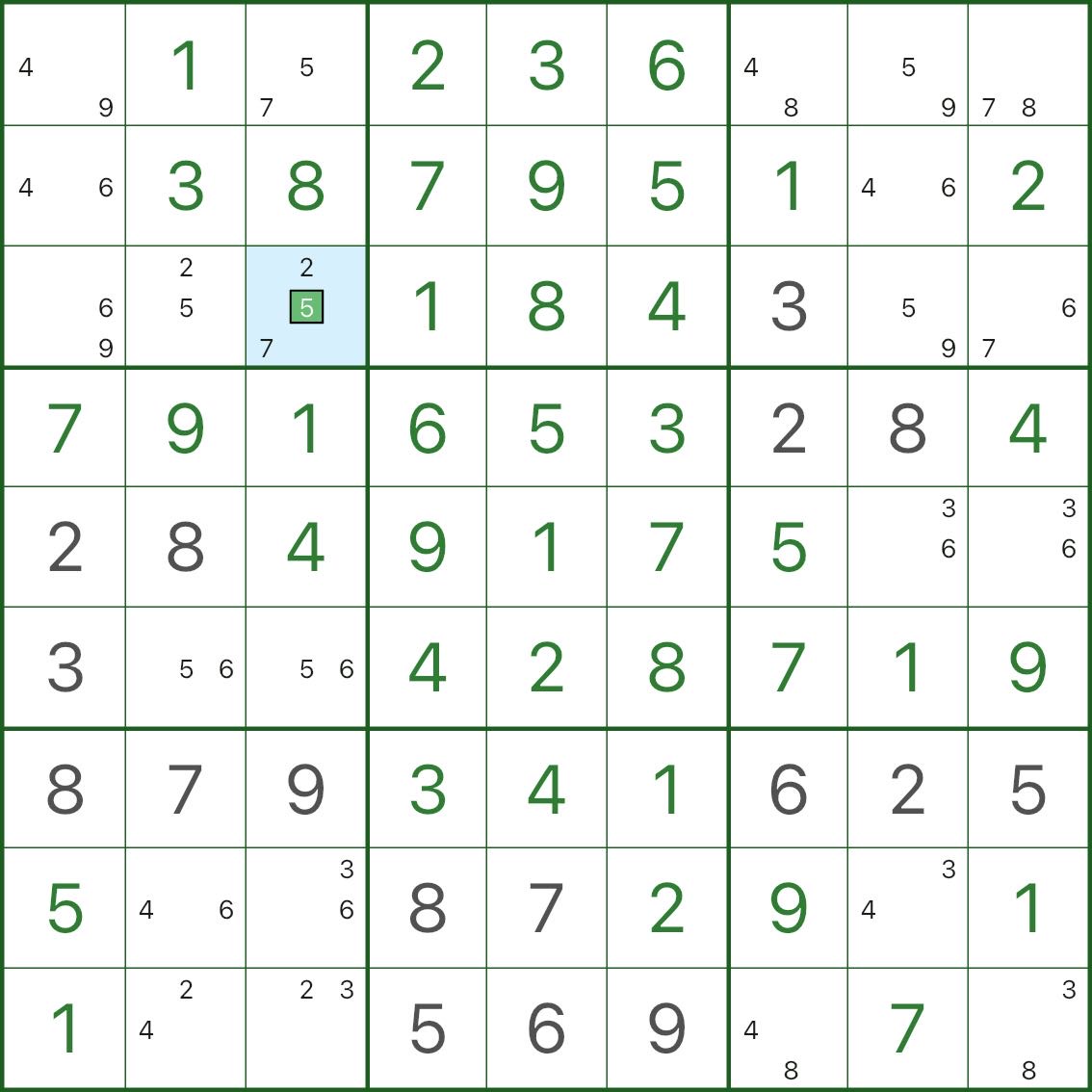
4. How to spot BUG+1

Use this checklist:

1. Make sure your candidate notes are complete and reliable (generate full candidates if needed)
2. Look for a grid where:
   • all unsolved cells are bivalue
   • exactly one cell has 3 candidates
3. In that cell’s row/column/box, count candidate occurrences for those three digits: the odd one (typically 3) is the forced digit
4. The hint will highlight the exception cell and show which candidate is forced

Note: BUG+1 is a uniqueness-based technique — it only applies when the puzzle is guaranteed to have a single solution.