XY-Flügel

Beschreibung

XY-Wing (auch bekannt als Y-Wing) ist eine kurze Kandidaten-Ausscheidungskette, die aus einem Drehpunkt und zwei Flügeln besteht.

Seine Form sieht so aus:

• Pivot (blau): genau zwei Kandidaten x, y
• Flügel (gelb): {x, z} und {y, z}

Fazit: Jede Zelle, die beide Flügel sehen kann, kann kein Z enthalten, daher kann der Kandidat z dort eliminiert werden.

---

Erklärung

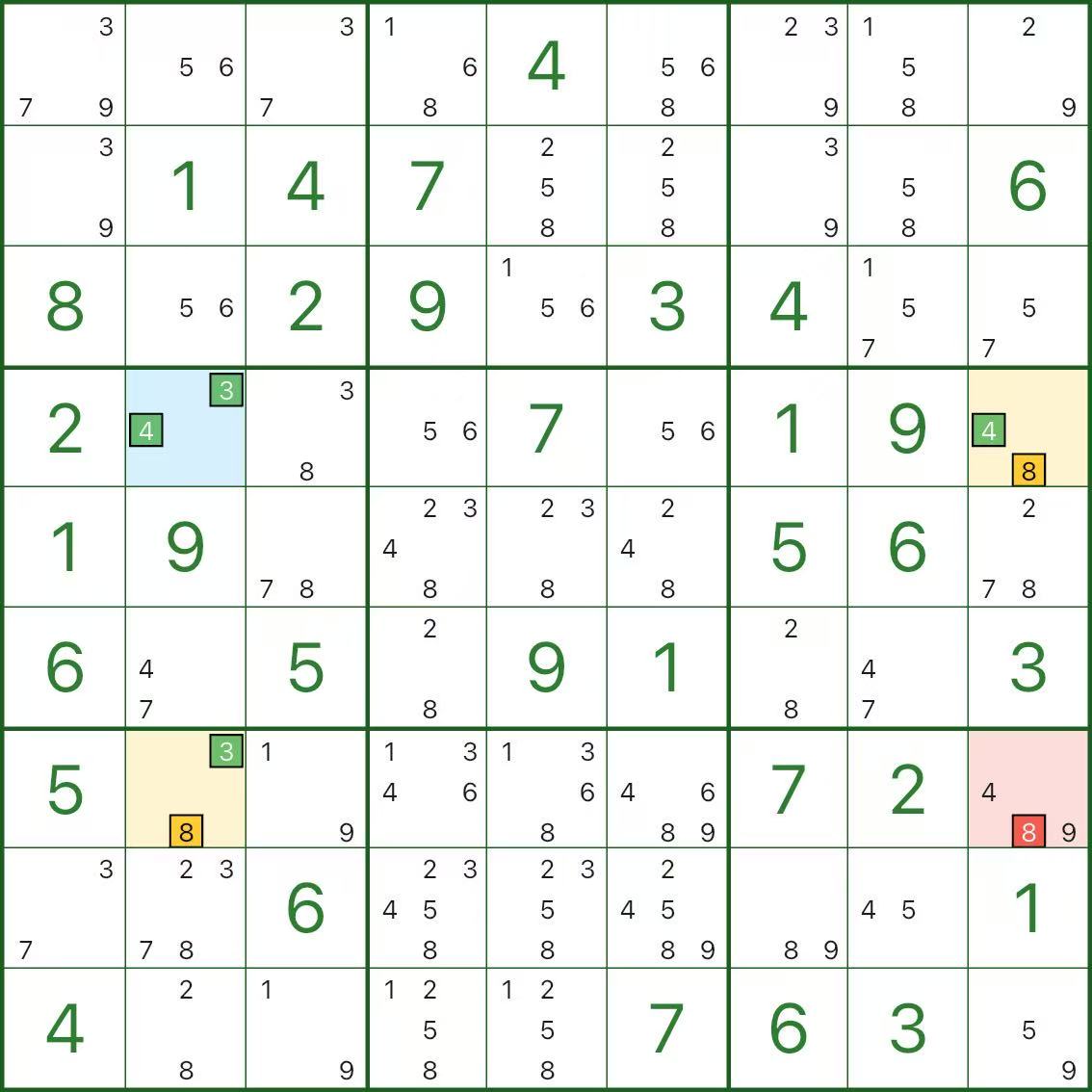
Im Bild oben wollen wir Kandidat 8 in r7c9 (rot) eliminieren.
Der blaue Pivot ist r4c2 mit den Kandidaten 3 und 4.
Die beiden gelben Flügel sind:

• r4c9: Kandidaten 4 und 8
• r7c2: Kandidaten 3 und 8

Warum können wir 8 aus r7c9 entfernen? Ein kurzer Widerspruch genügt:

• Angenommen r7c9 = 8 (der rote Kandidat ist wahr)
• r7c9 kann beide Flügel sehen, daher wird 8 aus beiden Flügeln eliminiert:
  • r4c9 muss 4 sein
  • r7c2 muss 3 sein
• Jetzt steckt der Pivot r4c2 fest:
  • r4c9 = 4 ⇒ r4c2 darf nicht 4 sein (gleiche Zeile)
  • r7c2 = 3 ⇒ r4c2 darf nicht 3 sein (gleiche Spalte)
  • r4c2 hatte nur {3,4} ⇒ kein Wert passt (Widerspruch)

Daher ist die Annahme unmöglich: r7c9 kann nicht 8 sein und der Kandidat 8 kann eliminiert werden.

---

Beispiele

Diese Bilder zeigen weitere XY-Wing-Muster. Versuchen Sie, die gleiche Struktur zu erkennen: Drehpunkt (blau) / zwei Flügel (gelb) / Eliminierung (rot).

---

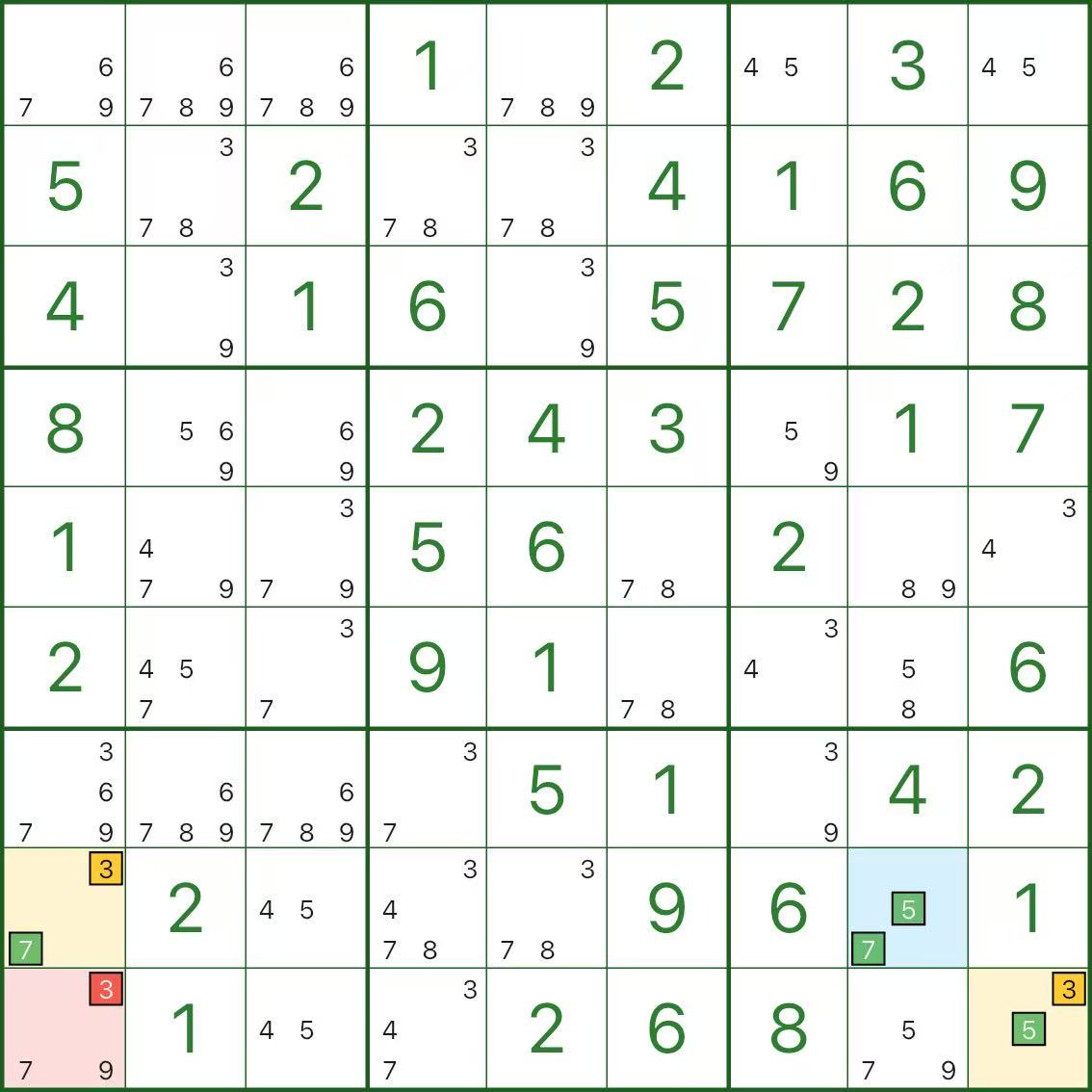
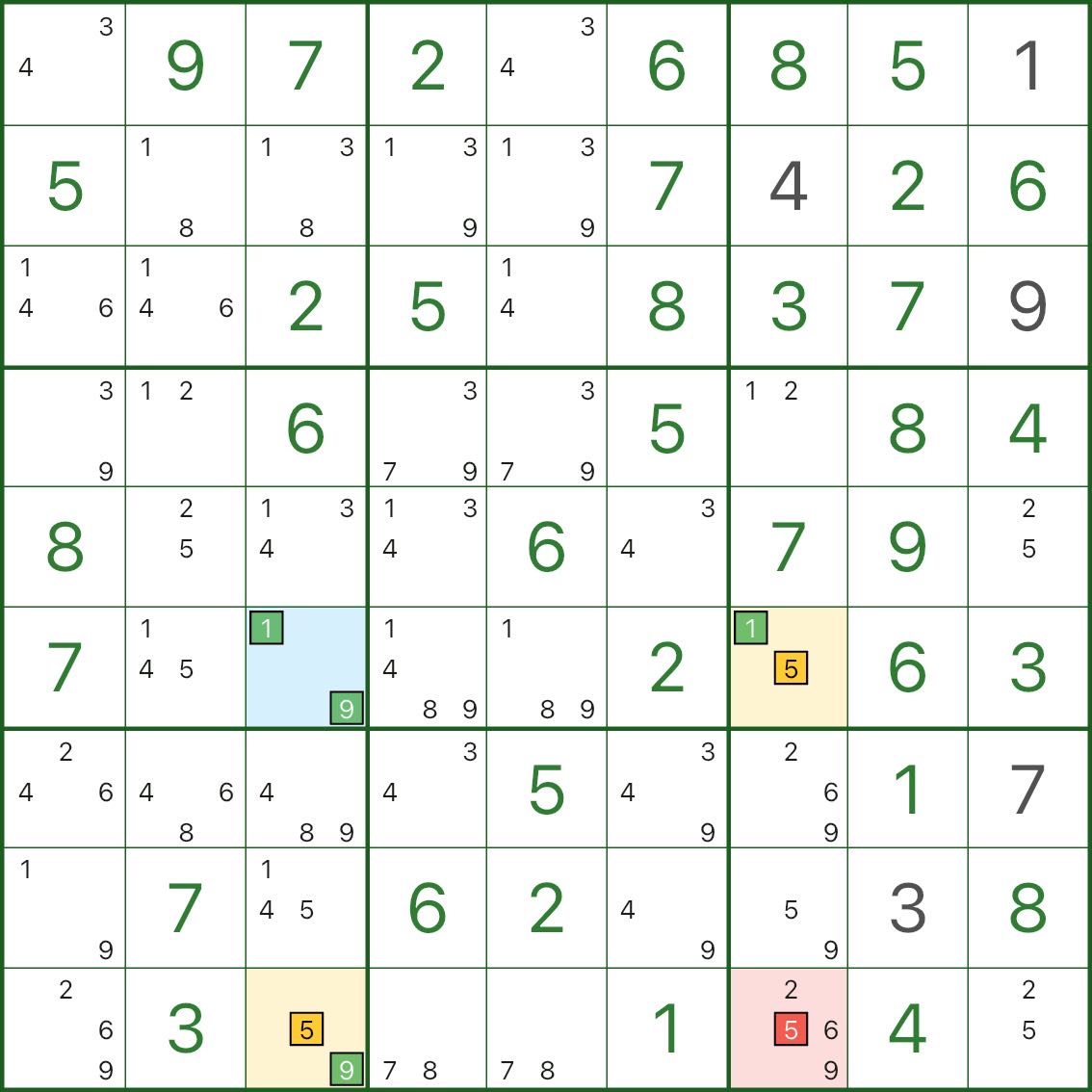
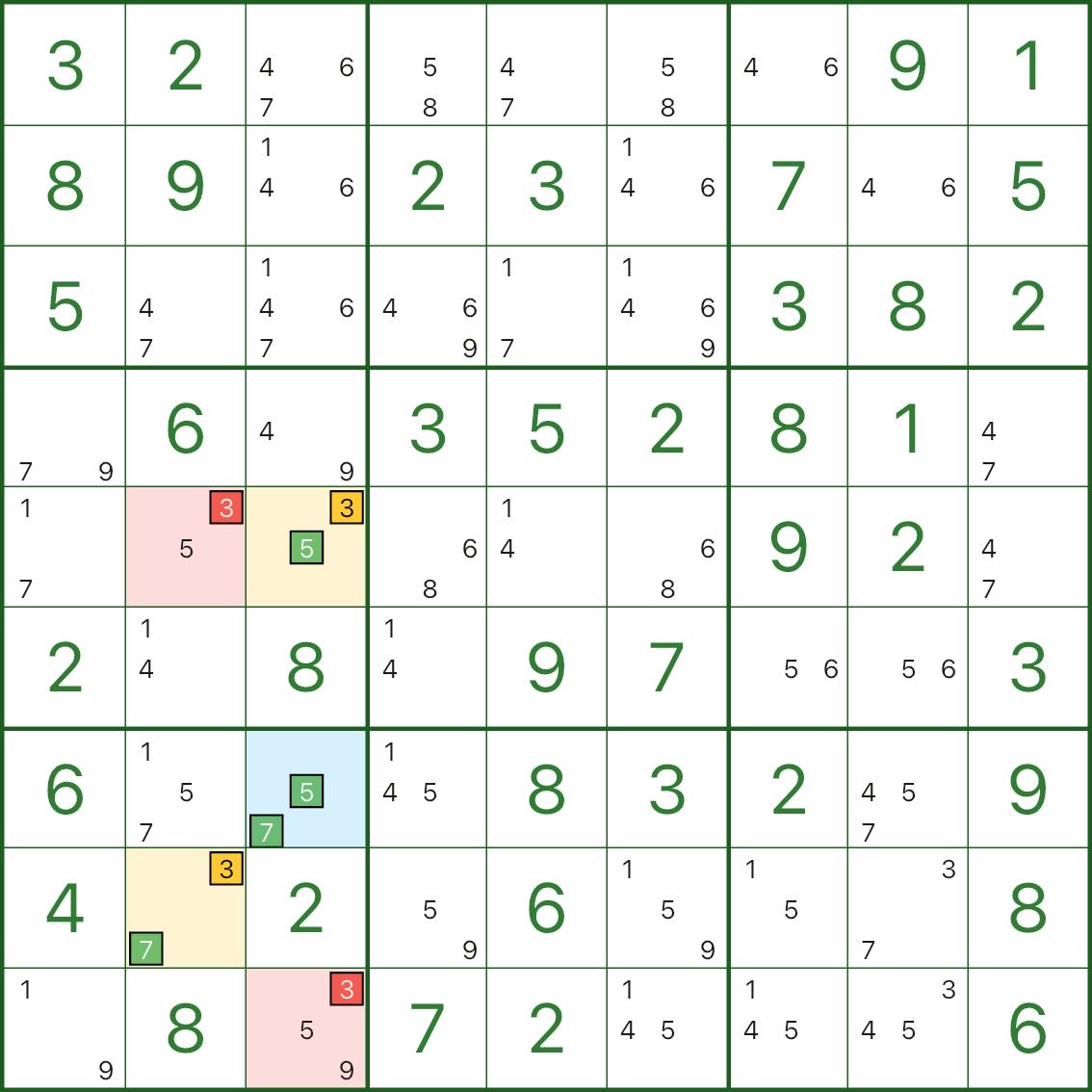
So finden Sie den XY-Wing

Einzeilige Checkliste: Suchen Sie einen Pivot mit zwei Kandidaten {x,y}, finden Sie zwei Flügel mit zwei Kandidaten {x,z} und {y,z} und entfernen Sie dann z aus jeder Zelle, die beide Flügel sieht.

In einem echten Puzzle:

1. Finden Sie eine Zelle mit genau zwei Kandidaten als Pivot (blau)
2. Finden Sie zwei Zellen, die den Pivot sehen können, jede mit genau zwei Kandidaten, geformt wie {x,z} und {y,z} (gelb)
3. Jede Zelle, die beide Flügel sehen kann, ist ein typischer Eliminierungspunkt: Entfernen Sie den Kandidaten z dort (rot)