Einzigartiges Rechteck (UR)

Voraussetzung: UR geht davon aus, dass das Rätsel genau eine Lösung hat.
Wenn Sie es noch nicht gelesen haben, beginnen Sie hier:
Uniqueness

---

1. Übersicht

Unique Rechteck (UR) ist eine Familie von Techniken, die die Eigenschaft single-solution verwenden, um Kandidaten zu eliminieren (und manchmal eine Zahl zu platzieren).

Es konzentriert sich auf eine „gefährliche Form“:

• Vier Zellen bilden ein 2×2-Rechteck (zwei Zeilen × zwei Spalten, die genau zwei Felder umfassen)
• alle vier Ecken enthalten die gleichen zwei Kernkandidaten (z. B. 1 und 7)

Wenn wir diese vier Zellen nur mit diesem Paar belassen, kann das Rechteck oft auf zwei verschiedene Arten gefüllt werden (durch Vertauschen der beiden Ziffern), was die Eindeutigkeit zerstören würde.
Unter der Eindeutigkeitsannahme können wir also schlussfolgern: Einige Kandidaten müssen entfernt werden oder eine Zelle muss einen bestimmten Wert annehmen.

---

2. Komplettlösung (5 Typen)

Die 5 Bilder unten entsprechen den 5 gängigen UR-Typen (in den In-App-Hinweisen werden sie als Typ I–V bezeichnet).

Farbratgeber:

• Blaue Zellen: das UR-Rechteck (die Kernstruktur)
• Gelbe Markierungen: Kandidaten, auf die wir uns in der Begründung konzentrieren
• Rote Markierungen: zu eliminierende Kandidaten / oder eine Zelle, die gesetzt werden kann

Typ I: Einzeldach → ein erzwungener Wert

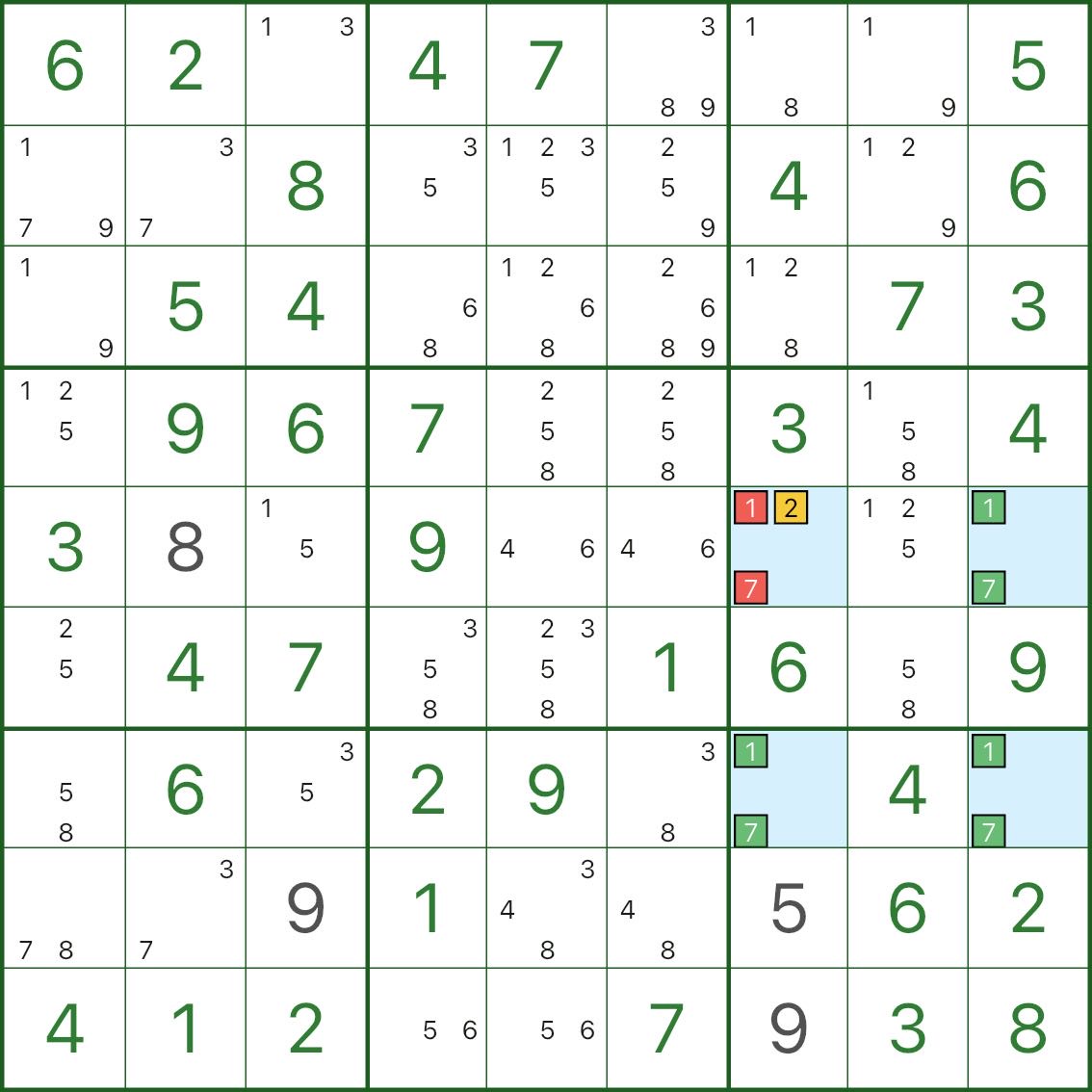
Schauen Sie sich die vier blauen Zellen an: Sie bilden ein Rechteck und enthalten alle die Kandidaten 1 und 7.
Zelle r5c7 hat auch einen zusätzlichen Kandidaten 2.

Wenn 2 in r5c7 nicht wahr ist, dann würde r5c7 nur noch 1 und 7 übrig haben.
Das würde alle vier Ecken „nur {1,7}“ machen und zwei austauschbare Füllungen ermöglichen (wodurch die Eindeutigkeit gebrochen würde).

Also unter Einzigartigkeit:

• r5c7 kann die Kandidaten 1 und 7 nicht behalten
• daher muss r5c7 2 sein

---

Typ II: zwei Dächer → c eliminieren, das beide Dächer sieht

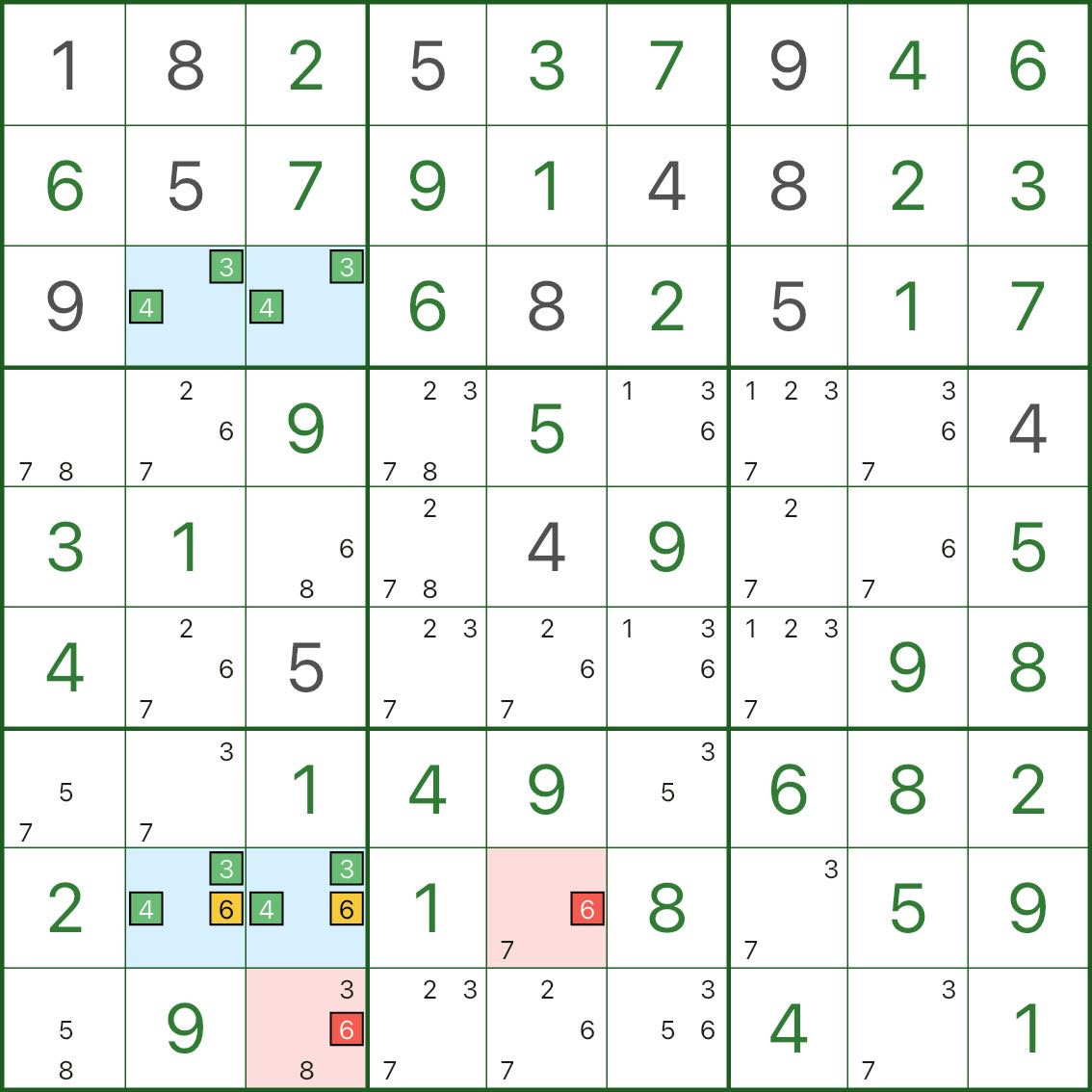
Hier basiert das blaue Rechteck auf den Kernkandidaten 3 und 4.
Zwei blaue Zellen r8c2 und r8c3 enthalten auch den Kandidaten 6 (also {3,4,6}).

Betrachten Sie nun einen roten Kandidaten 6 (zum Beispiel in r8c5 oder r9c3), der beide Dachzellen sehen kann:

• Wenn diese rote 6 wahr wäre, würden beide Dächer erzwungen, nicht 6
• Die Dächer würden nur noch auf {3,4} einstürzen
• Das Rechteck wird wieder zu einem tödlichen {3,4}-Muster (bricht die Einzigartigkeit)

Diese roten 6 Kandidaten können also nicht wahr sein und können eliminiert werden.

---

Typ III: Behandeln Sie die Dächer als „Paket“ und bilden Sie eine Teilmenge

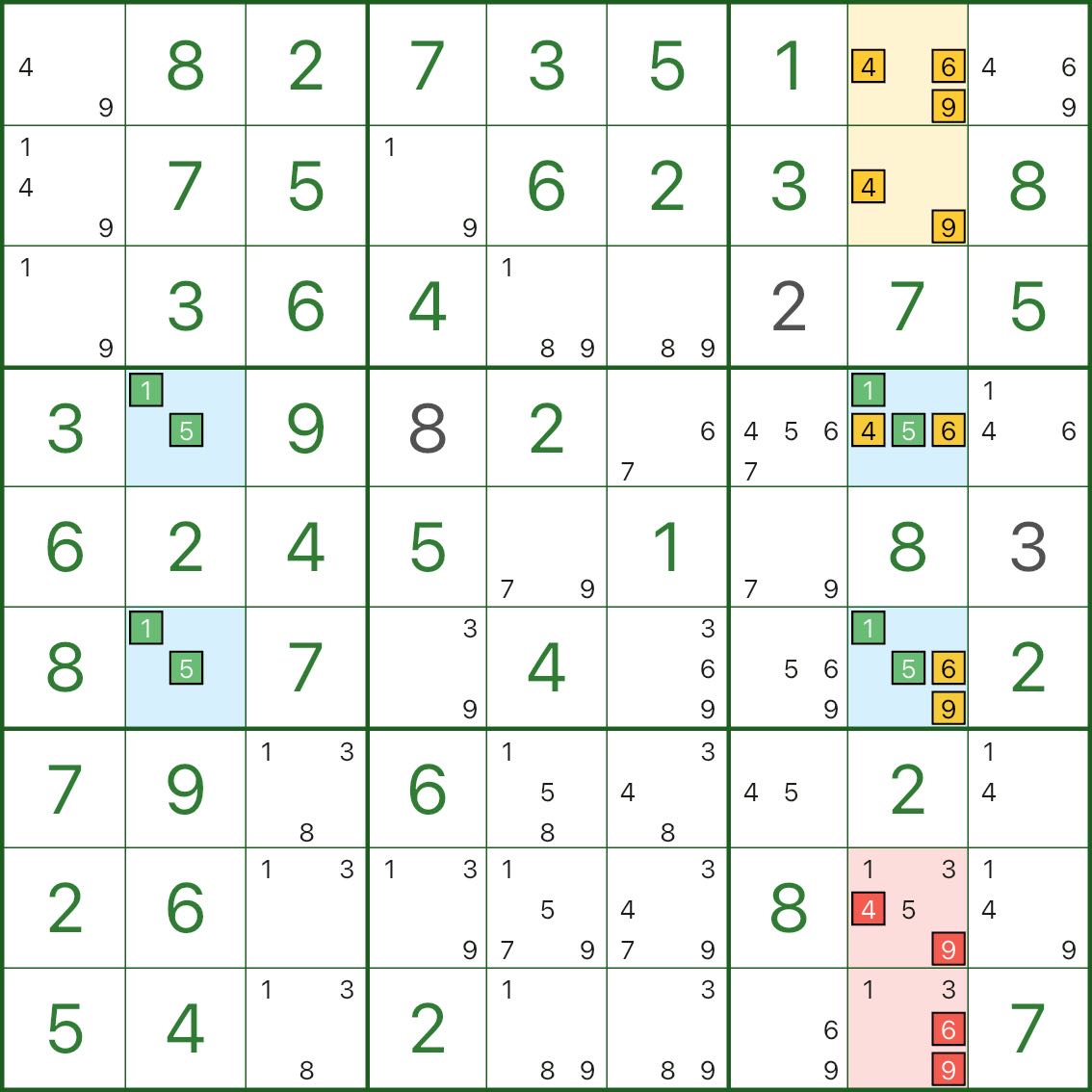
Dieser konzentriert sich auf Spalte 8:

• Zwei blaue Zellen in Spalte 8 enthalten beide die Kernkandidaten 1 und 5
• Sie teilen sich auch die zusätzlichen Ziffern 4, 6, 9 (jede ist also {1,5,4,6,9})

Einzigartigkeit erzwingt eine wichtige Einschränkung:

• Von diesen beiden blauen Feldern muss mindestens eines eine Ziffer aus {4,6,9} annehmen
• andernfalls würden sich beide nur auf {1,5} verlassen und das Rechteck in ein tödliches Muster verwandeln

Wir können also „die zusätzlichen Ziffern {4,6,9} der beiden blauen Zellen“ als Paket behandeln.
Zusammen mit den gelben Zellen r1c8 und r2c8 werden dadurch die Ziffern 4, 6, 9 effektiv in einer kleinen Teilmenge in Spalte 8 gesperrt.

Daher können alle anderen 4/6/9 Kandidaten in Spalte 8 (rot markiert) ausgeschlossen werden.

---

Typ IV: Ein konjugiertes Paar erzwingt eine Ziffer → eliminiert die andere

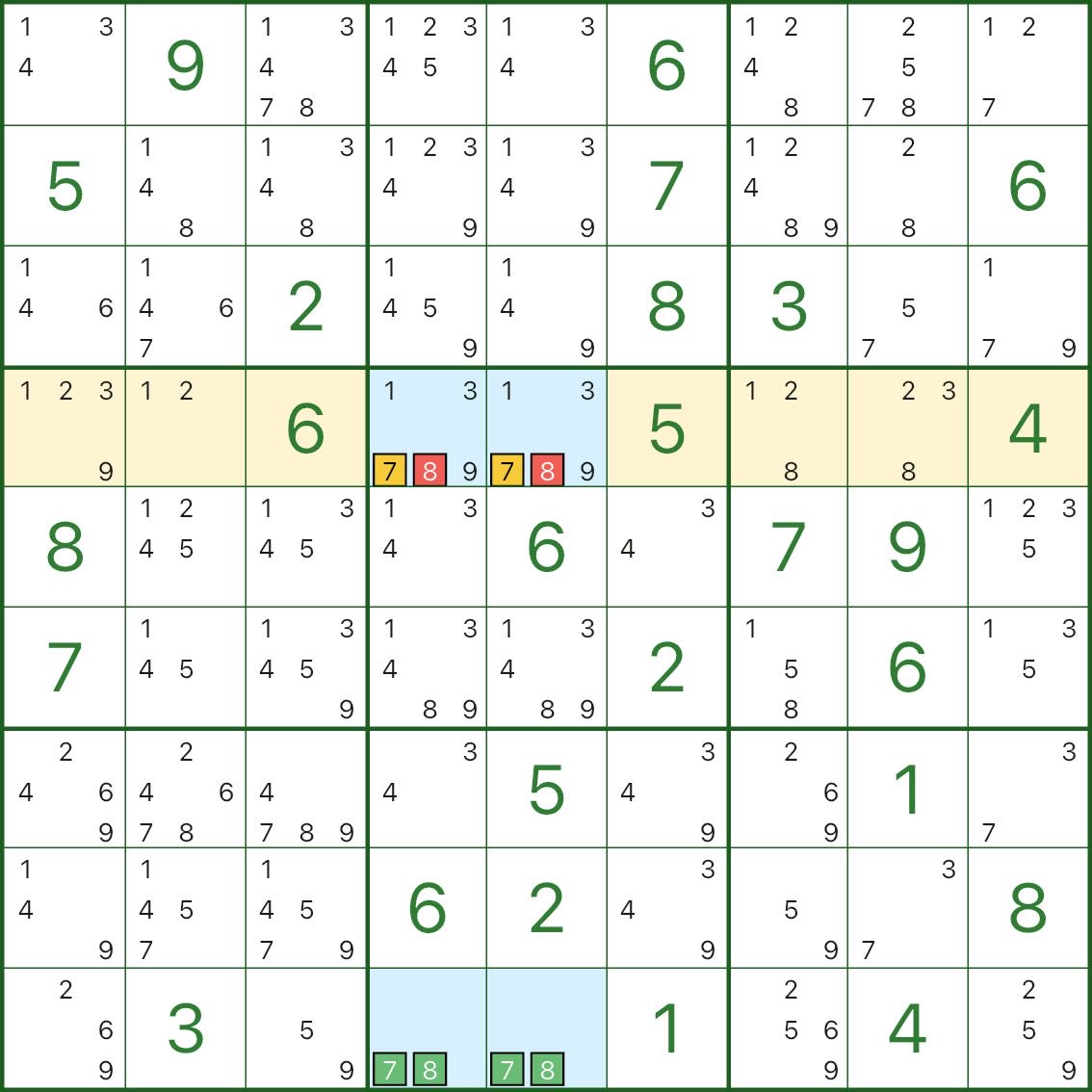
Das blaue Rechteck ist wieder auf einem Kernpaar aufgebaut (hier 7 und 8).In Zeile 4 erscheint Kandidat 7 nur in den beiden blauen Zellen r4c4 und r4c5.
Das bedeutet:

• Einer von r4c4 / r4c5 muss 7 sein

Mit dieser Einschränkung würde das Behalten des Kandidaten 8 in denselben blauen Zellen immer noch dazu führen, dass das Rechteck zu einer tödlichen Struktur zusammenbricht (wodurch die Einzigartigkeit zerstört wird).

So können wir 8 aus r4c4 und r4c5 eliminieren.

---

Typ V: mehrere Dächer (2 oder 3) → c eliminieren, das alle Dachzellen sieht

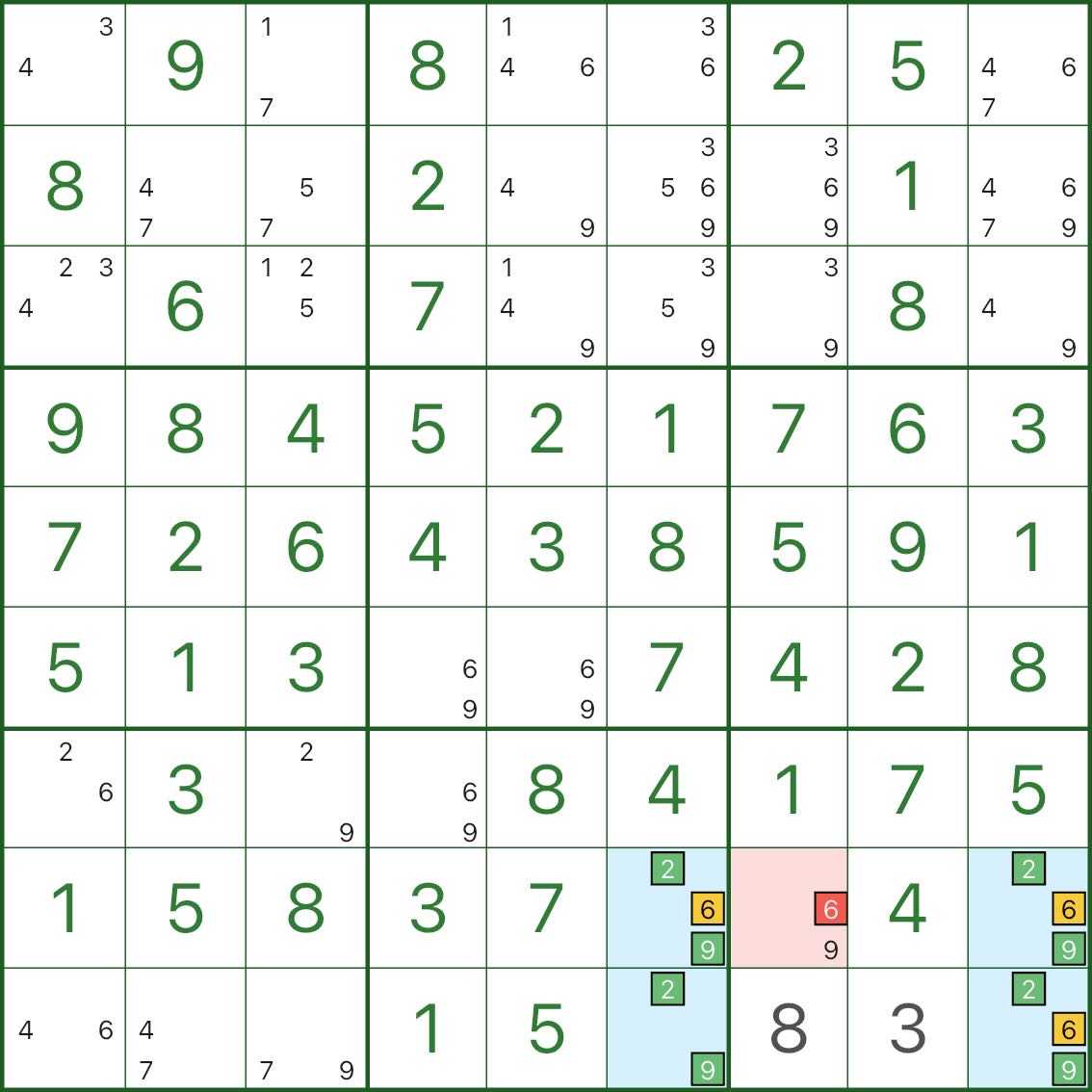
Beim Typ V handelt es sich nicht unbedingt um „drei Dächer“. Der Schlüsselgedanke ist:

• Es gibt 2 oder 3 Dachzellen im Rechteck, und alle haben denselben zusätzlichen Kandidaten c
• Wenn es nur 2 Dachzellen gibt, teilen sie sich normalerweise nicht dieselbe Zeile/Spalte/dieselben Kasten (wenn ja, dann handelt es sich eher um Typ II).
• Wenn der Kandidat c einer Zelle alle dieser Dachzellen sehen kann, dann kann dieses c nicht wahr sein und kann eliminiert werden

In diesem Bild umfasst das blaue Rechteck hauptsächlich die Ziffern 2, 6, 9:

• drei blaue Ecken sind {2,6,9}
• die verbleibende blaue Ecke ist {2,9} (es fehlen 6)

Schauen Sie sich nun die rote Zelle r8c7 an: Sie hat den Kandidaten 6 und kann alle {2,6,9} Dachzellen in diesem Muster sehen.

Wenn r8c7 = 6:

• alle drei Dachzellen wären zwangsweise nicht-6
• Sie würden nur zu {2,9} zusammenfallen
• Das Rechteck wird zu einem tödlichen {2,9}-Muster (bricht die Einzigartigkeit)

Der Kandidat 6 in r8c7 kann also nicht wahr sein und kann eliminiert werden.

---

3. Beispiele

Die Bilder 1–5 in diesem Artikel sind bereits Beispiele für Typ I–V.
Versuchen Sie beim Üben zuerst, das blaue Rechteck zu erkennen, und ordnen Sie dann die gelben/roten Markierungen der obigen Überlegung zu.

---

4. So erkennen Sie ein einzigartiges Rechteck

Bei echten Rätseln können Sie in dieser Reihenfolge suchen:

1. Suchen Sie nach vier leeren Zellen, die ein 2×2-Rechteck (zwei Zeilen × zwei Spalten) bilden und genau zwei Kästchen umfassen
2. Überprüfen Sie, ob alle vier Ecken dieselben zwei Kernkandidaten haben (das „tödliche Paar“)
3. Dann klassifizieren Sie die zusätzlichen Kandidaten danach, wie sie aussehen:
   • nur eine Ecke hat zusätzliche Kandidaten → Typ I (oft ein erzwungener Wert)
   • Zwei Ecken haben die gleiche zusätzliche Ziffer c → Typ II
   • Die zusätzlichen Ziffern der Dächer können eine Teilmenge in einer Zeile/Spalte/Box bilden → Typ III
   • In einem Haus kommt eine Kernziffer nur in zwei Rechteckzellen vor → Typ IV
   • zwei oder drei Ecken teilen sich die gleiche zusätzliche Ziffer c (bei zwei Dächern teilen sie sich normalerweise kein Haus) → Typ V

Das ist UR in einem Satz: Lassen Sie niemals zu, dass das Rechteck in ein tödliches Muster zusammenfällt – sonst würde die Einzigartigkeit zerstört.