Paare und Teilmengen

Nackte/verborgene Paare und Teilmengen

Paare und Teilmengen gehören zu den nützlichsten Techniken zur „Kandidateneliminierung“. Sie haben unterschiedliche Namen, aber sie machen alle dasselbe:

In einem Haus (einer Zeile/Spalte/einem Feld) „reservieren“ ein kleiner Satz von Zellen und ein kleiner Satz von Ziffern die Plätze füreinander – sodass diese Ziffern nicht an anderer Stelle in diesem Haus erscheinen können.

Sie müssen sich den Jargon nicht merken. Eine einfache Faustregel:

• Nackt: Beginnen Sie mit dem, was die Zellen anzeigen (diese Zellen enthalten nur diese Ziffern)
• Versteckt: Beginnen Sie dort, wo eine Ziffer stehen kann (diese Ziffern können nur in diesen Zellen stehen)

---

1. Nacktes Paar

Wenn im selben Haus zwei Zellen beide nur die gleichen zwei Kandidaten enthalten (z. B. {a,b}), haben Sie ein nacktes Paar.

Das bedeutet:

• Eine Zelle muss a sein, die andere muss b sein (Reihenfolge unbekannt)
• Die Kandidaten a und b können also aus jeder anderen leeren Zelle in diesem Haus entfernt werden

Schauen Sie sich zunächst das Bild unten an: Konzentrieren Sie sich auf das hervorgehobene Feld 3 und die beiden grünen Zellen r2c9 und r3c9.
Sie werden feststellen, dass sie nur {1,5} sein können.

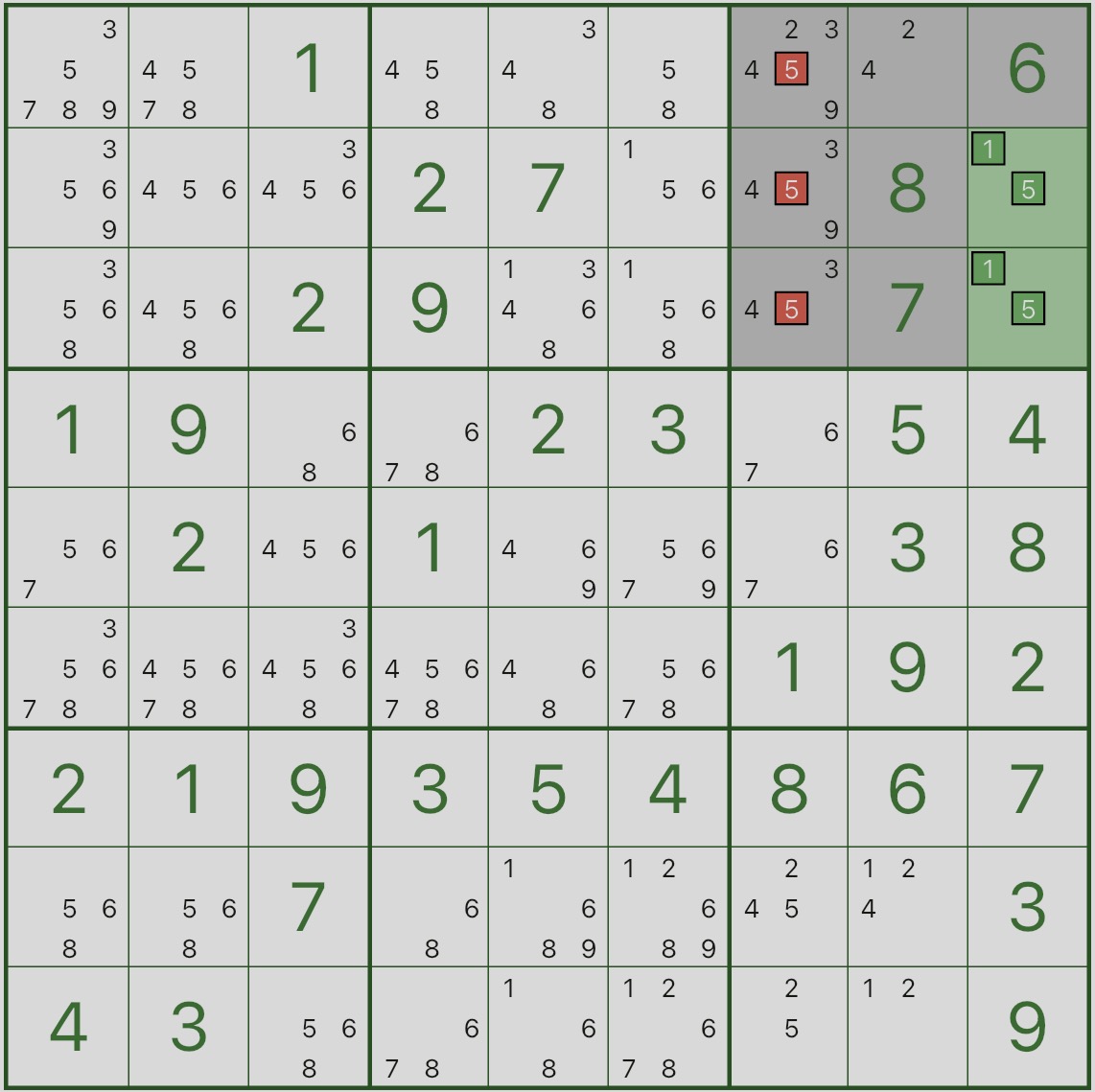
Das bedeutet: In Box 3 sind die Ziffern 1 und 5 „reserviert“ für r2c9 und r3c9.

Schauen Sie sich nun die roten Kandidaten an: Der Kandidat 5 in r1c7, r2c7, r3c7 kann entfernt werden.

Ein kurzer Widerspruchsbeweis:

• Angenommen, r1c7 ist 5 (die gleiche Logik gilt für r2c7 und r3c7)
• Dann enthält Box 3 bereits eine 5, daher können r2c9 und r3c9 nicht 5 sein und müssen zwangsweise 1 sein
• Aber r2c9 und r3c9 teilen sich dieselbe Spalte (Spalte 9), daher können sie nicht beide 1 sein – Widerspruch
  ⇒ Diese roten 5 Kandidaten sind unmöglich und können entfernt werden

---

2. Verstecktes Paar

Wenn im selben Haus der Kandidat a in genau zwei Zellen vorkommt und der Kandidat b auch in den gleichen zwei Zellen vorkommt, haben Sie ein verstecktes Paar.

In diesen beiden Zellen werden möglicherweise zusätzliche Kandidaten angezeigt, a und b sind jedoch bereits für sie gesperrt, sodass Sie Folgendes tun können:

• Entfernen Sie alle Kandidaten außer a und b aus diesen beiden Zellen

Schauen Sie sich zunächst das Bild unten an: Konzentrieren Sie sich auf die hervorgehobene Spalte 4.
Finden Sie heraus, wo die Kandidaten 4 und 5 in dieser Spalte erscheinen – Sie werden sehen, dass sie nur in r1c4 und r6c4 erscheinen.

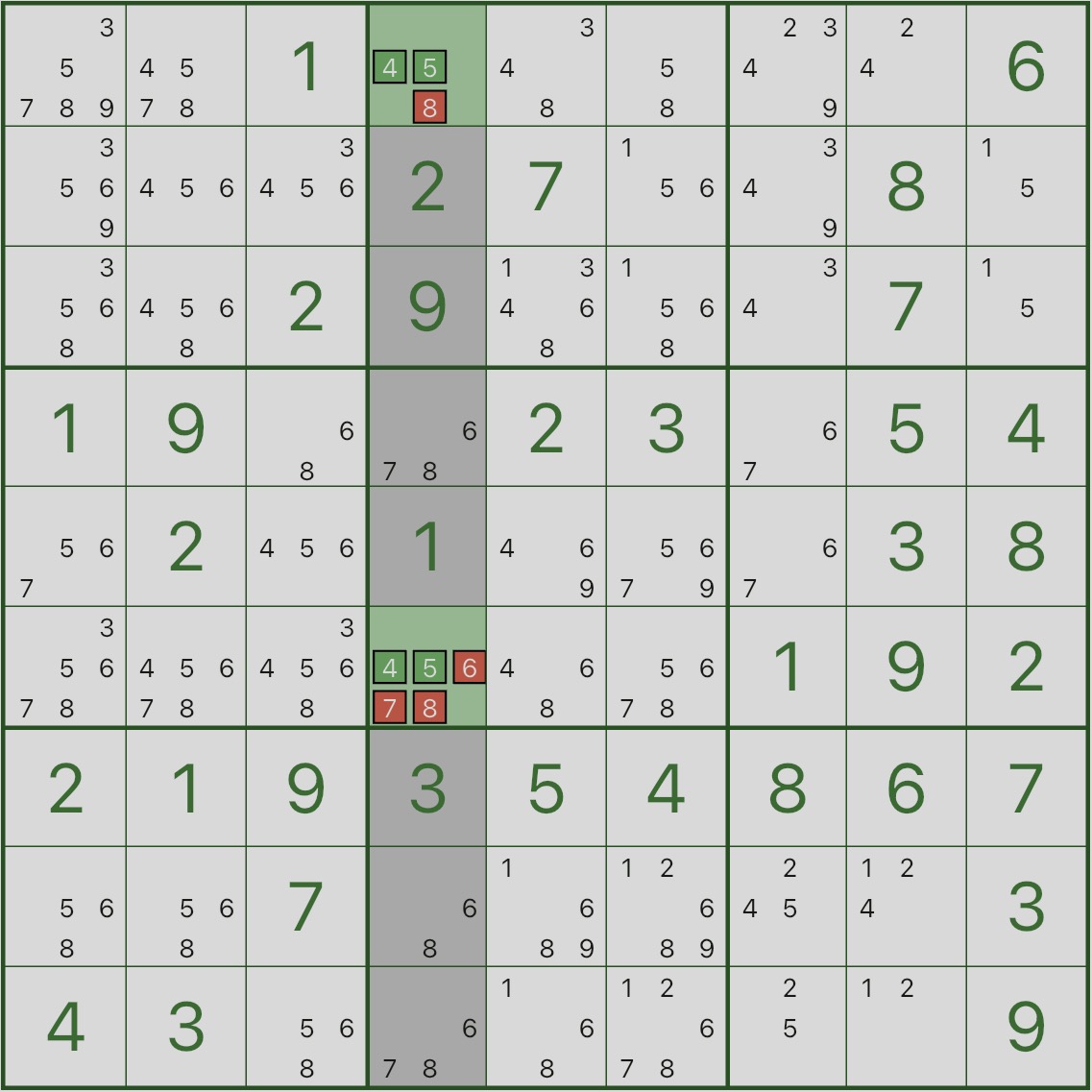
Das bedeutet: In Spalte 4 müssen die Ziffern 4 und 5 in r1c4 und r6c4 platziert werden.

Warum können wir andere Kandidaten aus r1c4 und r6c4 entfernen?

• Angenommen, r1c4 nimmt eine Ziffer an, die nicht 4 oder 5 ist
• Dann müssten sowohl 4 als auch 5 in nur r6c4 passen
• Eine einzelne Zelle kann nicht gleichzeitig 4 und 5 sein – ein Widerspruch
  ⇒ r1c4 und r6c4 müssen {4,5} sein, damit andere Kandidaten in diesen Zellen entfernt werden können

---

3. Nackte Teilmenge (Triple / Quad)

Dies ist die Idee des „nackten Paares“, verallgemeinert:

Wenn N Zellen in einem Haus insgesamt nur N Ziffern enthalten (zum Beispiel enthalten drei Zellen nur {a,b,c}), haben Sie ein nacktes Tripel. Die gleiche Idee gilt für Quads.

Diese Ziffern müssen in diesen N Zellen platziert werden, also:

• Entfernen Sie diese Ziffern (z. B. a, b, c) aus jeder zweiten leeren Zelle in diesem Haus

Schauen Sie sich zunächst das Bild unten an: Konzentrieren Sie sich auf die hervorgehobene Zeile 8 und die drei Zellen r8c1, r8c2, r8c4.
Sie werden feststellen, dass diese drei Zellen zusammen nur {5,6,8} enthalten.

Das bedeutet: In Zeile 8 müssen die Ziffern 5, 6, 8 innerhalb von r8c1, r8c2, r8c4 platziert werden.

Deshalb können die roten Kandidaten 5, 6, 8 im Rest der Reihe 8 entfernt werden.

Eine einfache Widerspruchsansicht:

• Wenn eine andere Zelle in Zeile 8 eine von {5,6,8} „nimmt“
• Dann müssten diese drei Zellen mit nur zwei Ziffern für drei Zellen ausgefüllt werden
• Das kann nicht funktionieren – Widerspruch

---

4. Versteckte Teilmenge (Triple / Quad)

Dies ist die Idee des „verborgenen Paares“, verallgemeinert:

Wenn N Ziffern in einem Haus nur in denselben N Zellen vorkommen (auch wenn diese Zellen zusätzliche Kandidaten enthalten), haben Sie ein verstecktes Dreier-/Vierfach.

Diese N Ziffern sind an diese N Zellen gebunden, also:

• Entfernen Sie alle Kandidaten außer diesen N Ziffern aus diesen Zellen

Schauen Sie sich zunächst das Bild unten an: Konzentrieren Sie sich auf die hervorgehobene Spalte 5.
Sie werden feststellen, dass die Ziffern 4,7,8 nur in r1c5, r8c5, r9c5 vorkommen.

Das bedeutet: In Spalte 5 müssen die Ziffern 4, 7, 8 innerhalb von r1c5, r8c5, r9c5 platziert werden.

Daher können wir in diesen drei Zellen alle anderen Kandidaten entfernen, die nicht 4, 7 oder 8 sind.

Warum ist das sicher?

• Wenn eine dieser Zellen eine andere Ziffer hat
• Dann hätten 4, 7 und 8 weniger als drei passende Stellen – Widerspruch

---

5. Tipps, um sie schneller zu erkennen

• Sorgen Sie dafür, dass die Kandidaten einigermaßen vollständig sind (Sie werden sie für schwierigere Rätsel benötigen)
• Suchen Sie zuerst nach nackten Mustern: Beginnen Sie mit Zellen mit sehr wenigen Kandidaten (2, 3 oder 4).
• Suchen Sie dann nach versteckten Mustern: Überprüfen Sie in einem Haus, ob eine Ziffer auf 2, 3 oder 4 Stellen beschränkt ist
• Halten Sie nach dem Ausscheiden inne und schauen Sie noch einmal hin – vereinfachte Kandidaten verraten oft den nächsten Schritt