3D-Medusa (Erweiterte Färbung)

Voraussetzung: Basic Coloring

Übersicht

3D Medusa ist eine „verbesserte Farbgebung“-Technik: Sie verwendet immer noch zwei Farben (blau/gelb), um zwei sich gegenseitig ausschließende Deduktionswege darzustellen, konzentriert sich jedoch nicht mehr nur auf eine Ziffer – sie kann mehrere Ziffern in einem Argumentationsnetzwerk verbinden.

Was es stärker macht, ist, dass es mehr als eine Art starker Verbindung verwendet:

• Konjugiertes Paar (starker Link): In einer Zeile/Spalte/Box hat eine Ziffer genau 2 Kandidatenpositionen
• Zweiwertige Zelle (starker Link): Eine Zelle hat genau 2 Kandidaten

Nachdem Sie starke Links eingefärbt haben, können Sie sich Blau/Gelb als zwei gegensätzliche Annahmen vorstellen:

• Angenommen, Blau ist wahr ⇒ Gelb ist falsch
• Angenommen, Blau ist falsch ⇒ Gelb ist wahr

Innerhalb derselben Farbkomponente muss also eine der beiden Farben wahr sein.

3D-Medusa liefert am häufigsten zwei Arten von Schlussfolgerungen:

1. Falle: Ein roter Kandidat kollidiert sowohl mit der blauen als auch mit der gelben Route → eliminiere den roten Kandidaten
2. Widerspruch gleicher Farbe: Zwei gleichfarbige Kandidaten kollidieren in einem Haus (oder einer Zelle) → die gesamte Farbe ist unmöglich und kann eliminiert werden

Wenn Sie mit starken/schwachen Links noch nicht vertraut sind, lesen Sie: Chain Basics.

---

Falle

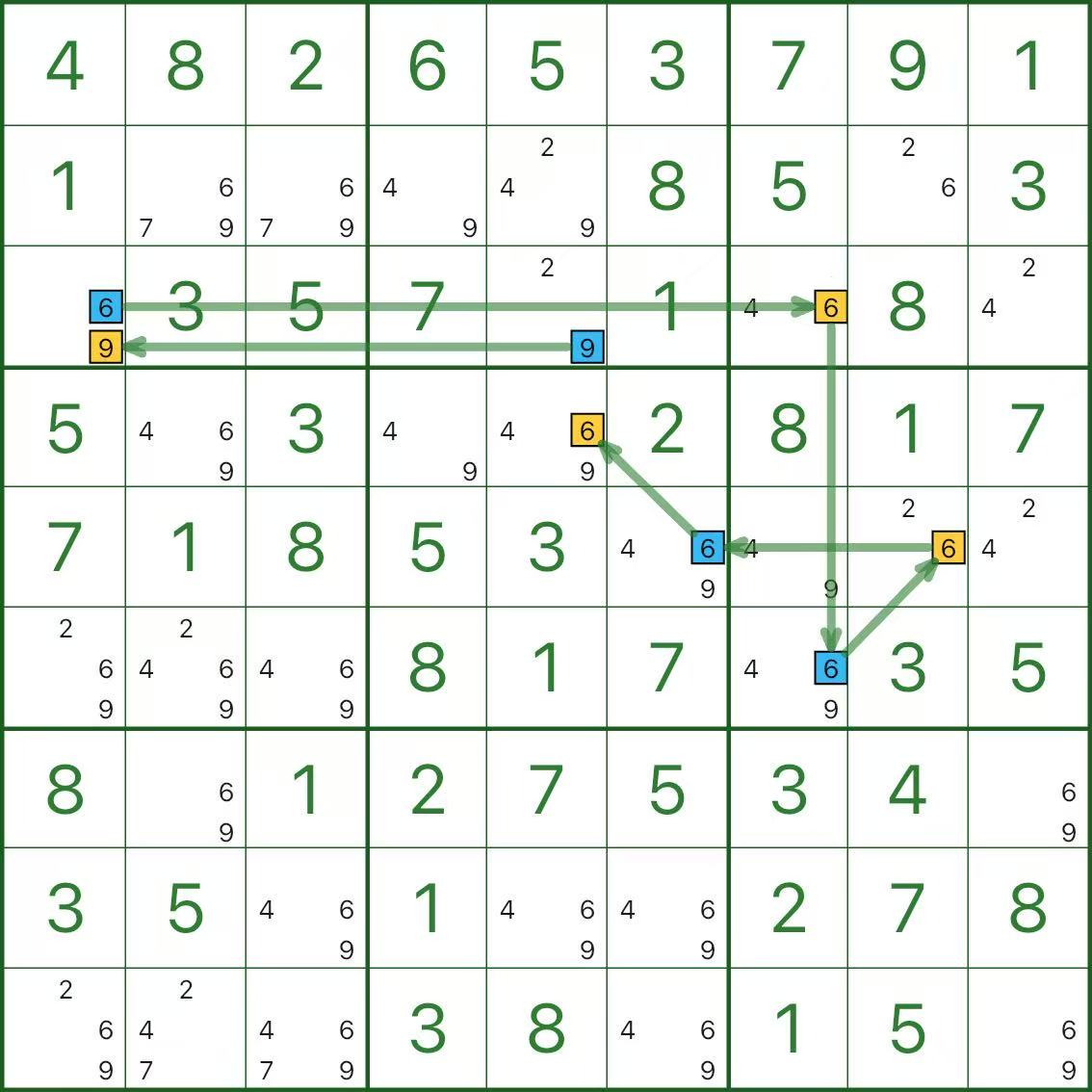
Im Bild oben färben wir Kandidaten entlang starker Links ein. Die Kette umfasst Kandidaten 9 in r3c5 (blau) und erreicht auch Kandidaten 6 in r4c5 (gelb).

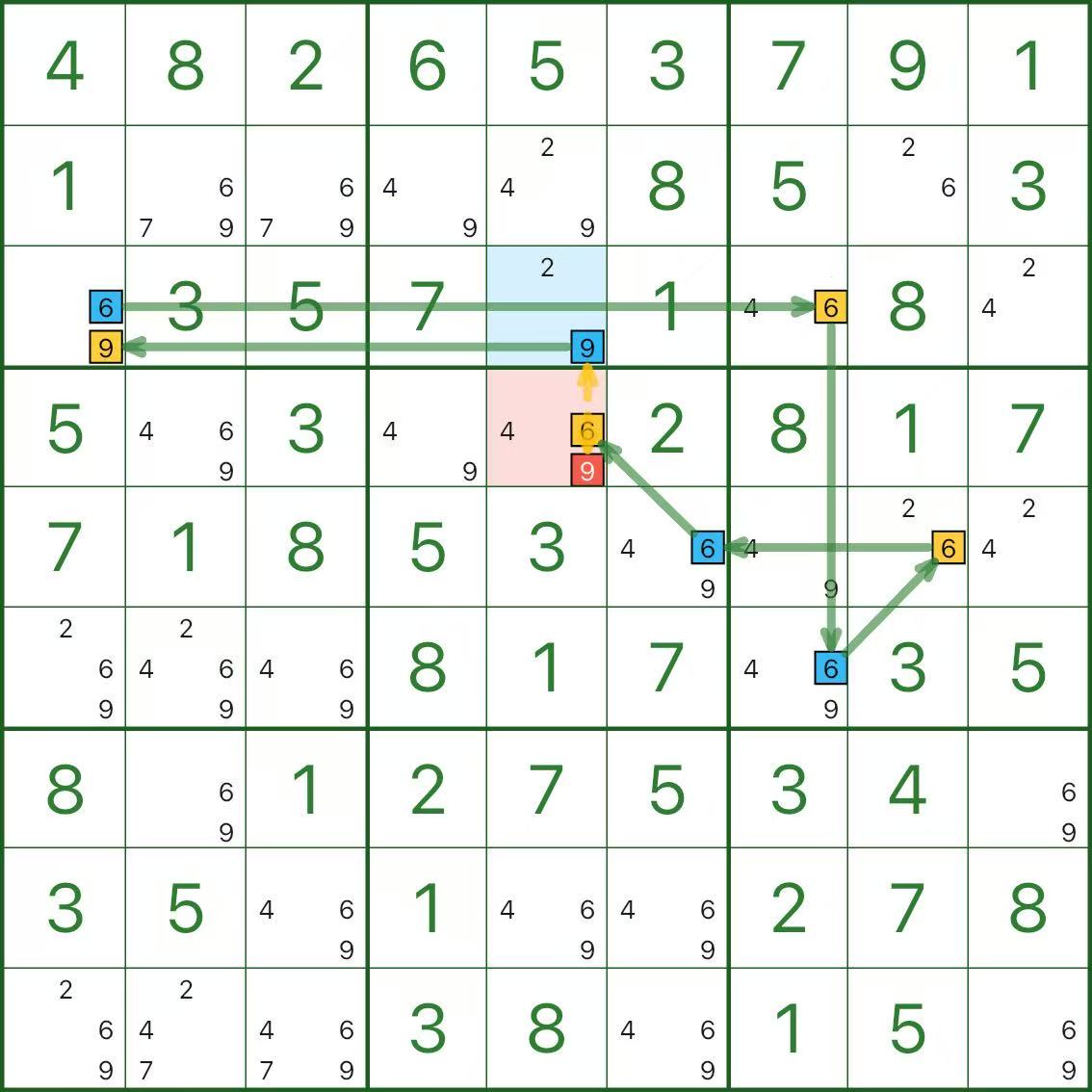
Im Bild oben ist der zu eliminierende rote Kandidat Kandidat 9 in r4c5.
Warum können wir es entfernen? Der Schlüsselgedanke lautet: „Eine der beiden Farben muss wahr sein“:

• Wenn blau wahr ist, dann ist der blaue Kandidat 9 in r3c5 wahr, sodass der rote Kandidat 9 in r4c5 damit in Konflikt steht und nicht wahr sein kann.
• Wenn blau falsch ist, muss die gelbe Route wahr sein; Da Kandidat 6 in r4c5 (gelb) wahr ist, kann r4c5 nicht auch 9 (gleiche Zelle) sein, sodass der rote Kandidat 9 in r4c5 immer noch nicht wahr sein kann.

In jedem Fall ist der rote Kandidat unmöglich und kann daher eliminiert werden.

---

Gleichfarbiger Widerspruch

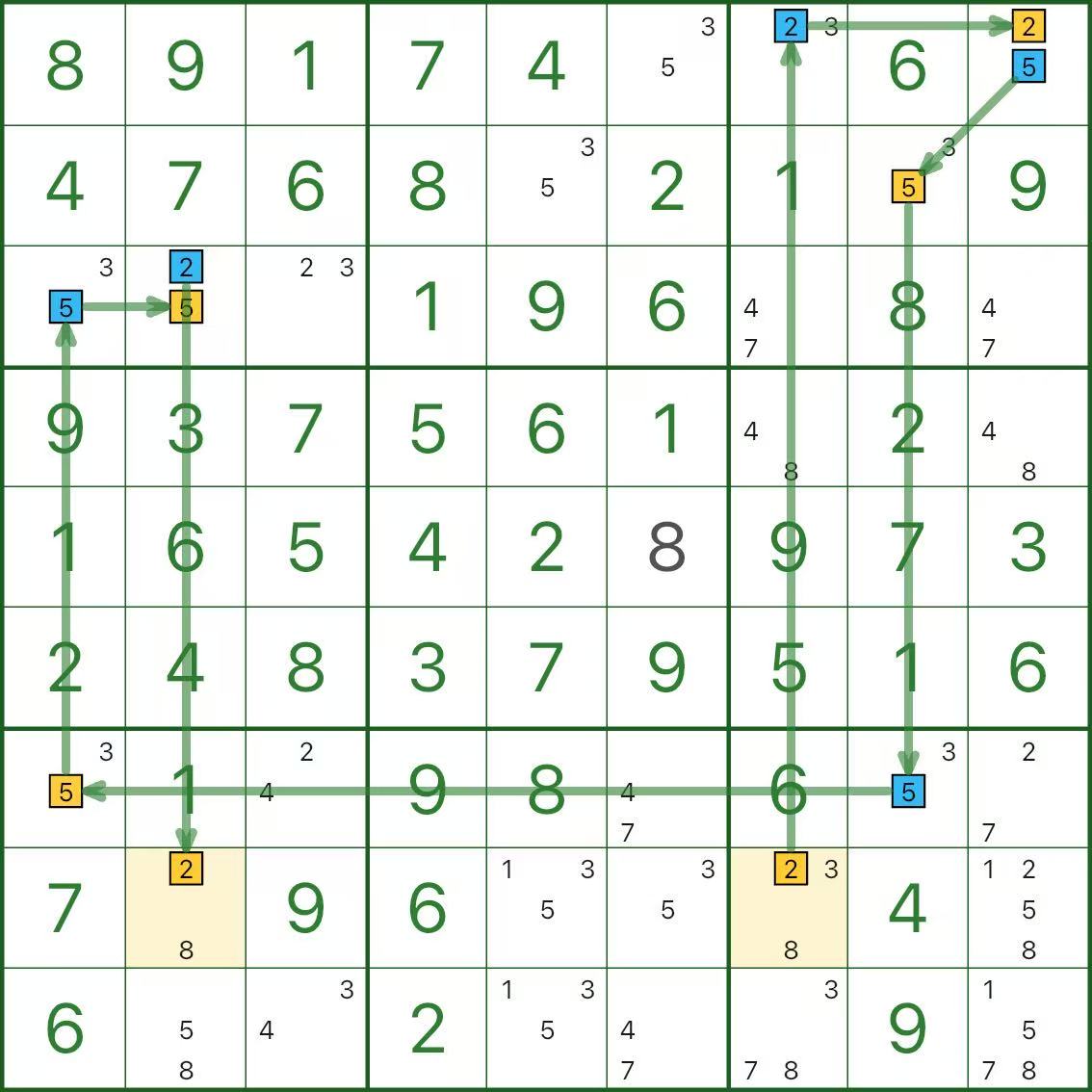
Im Bild oben sind Kandidat 2 in r8c2 und Kandidat 2 in r8c7 beide gelb gefärbt.
Aber sie befinden sich in derselben Reihe, also können sie nicht beide 2 sein – das ist ein Widerspruch gleicher Farbe.

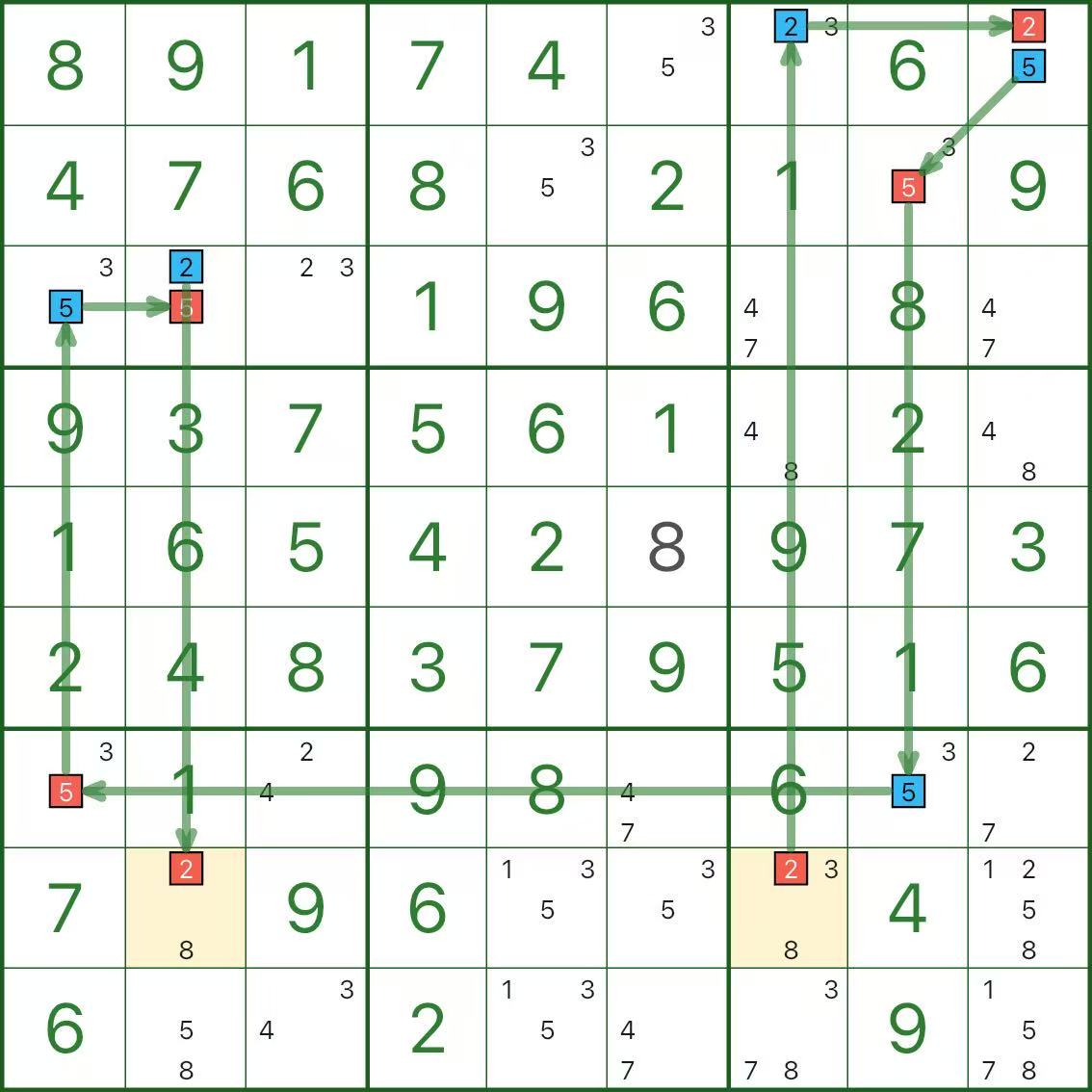
Daher ist die gelbe Route unmöglich und alle gelben Kandidaten in dieser farbigen Komponente können eliminiert werden (sie sind im Bild rot markiert).

---

So finden Sie die 3D-Medusa

Einzeilige Checkliste: Bauen Sie ein starkes Netzwerk auf (konjugierte Paare + zweiwertige Zellen), färben Sie es blau/gelb und suchen Sie dann nach Fallen oder gleichfarbigen Widersprüchen.

In einem echten Puzzle:

1. Finden Sie starke Verbindungen aus konjugierten Paaren und bivalenten Zellen
2. Farbkandidaten entlang starker Links (blau/gelb schließen sich gegenseitig aus)
3. Suchen Sie nach:
   • ein roter Kandidat, der mit beiden Farbrouten in Konflikt steht → Fallenbeseitigung
   • zwei gleichfarbige Kandidaten, die in einer Zeile/Spalte/einem Feld (oder einer Zelle) in Konflikt geraten → die gesamte Farbe eliminieren