Leeres Rechteck

> Voraussetzung: [Chain Basics](learning://chains)

Advanced

Leeres Rechteck

Voraussetzung: Chain Basics

Beschreibung

„Leeres Rechteck“ ist eine einstellige Kandidateneliminierungstechnik: Konzentrieren Sie sich auf eine Ziffer d.

Innerhalb eines Kästchens kann die Ziffer d eine spezielle Kreuz-/L-förmige Verteilung bilden – was bedeutet, dass alle d-Kandidaten in diesem Kästchen in einer Zeile und einer Spalte liegen.
Wenn eine kurze Kette d auf diese Linien zwingt, kann es manchmal zu einem sehr klaren Widerspruch kommen: Die Box hat am Ende keinen Platz für d, also muss die ursprüngliche Annahme falsch sein.

Erklärung

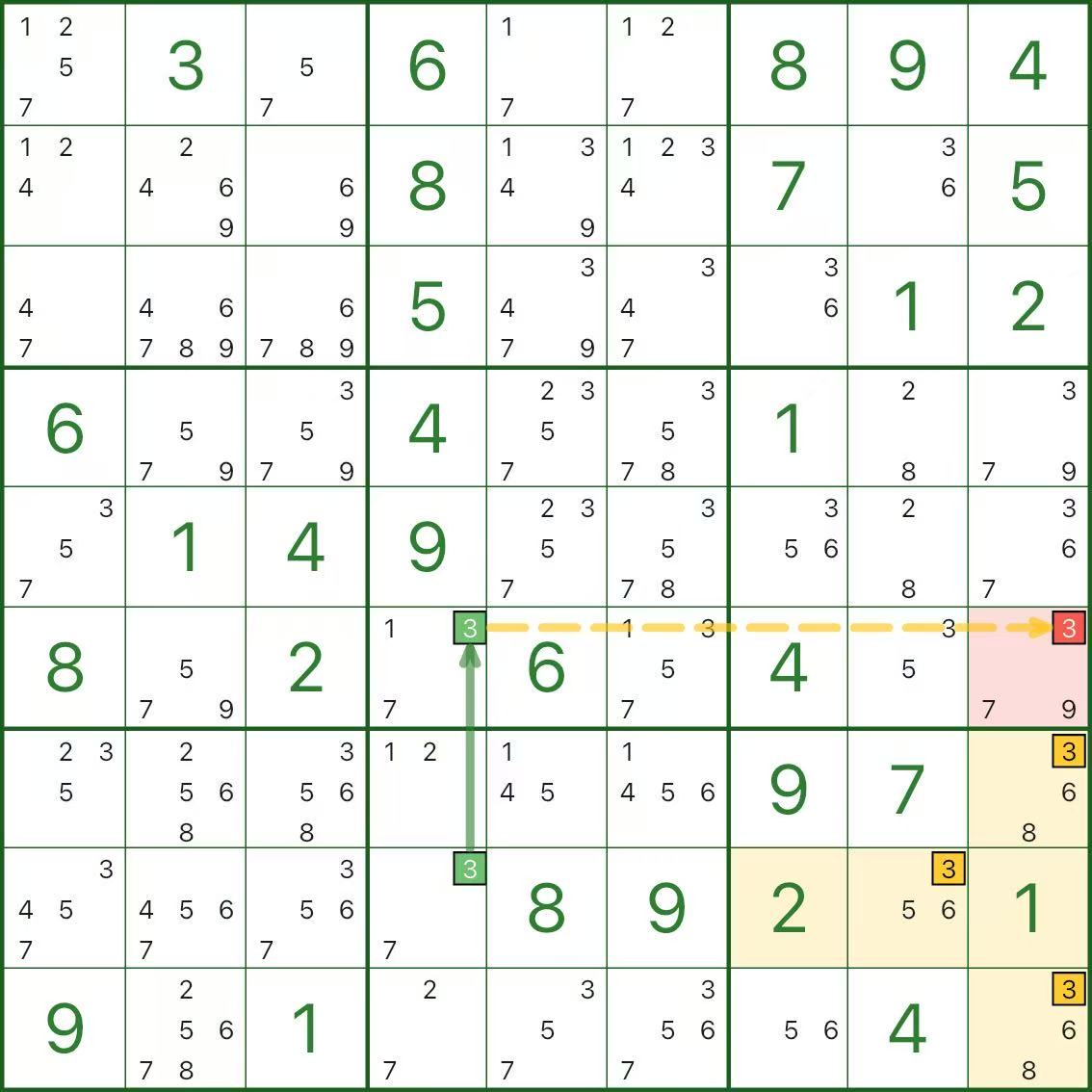
Empty Rectangle walkthrough example

Im Bild oben wollen wir Kandidat 3 in r6c9 (rot) eliminieren.

Hier der kurze Widerspruch:

Angenommen r6c9 = 3 (der rote Kandidat ist wahr)
Eine Zeile darf nicht zwei 3er enthalten, also r6c4 ≠ 3
In Spalte 4 hat Ziffer 3 nur zwei mögliche Zellen: r6c4 oder r8c4
Da r6c4 nicht 3 ist, muss r8c4 3 sein
Schauen Sie sich nun Box 9 (die leere rechteckige Box) an:
mit r6c9 = 3 (gleiche Spalte) und r8c4 = 3 (gleiche Zeile) werden alle verbleibenden 3 Positionen in Feld 9 eliminiert, sodass Feld 9 keinen Platz für Ziffer 3 hat (Widerspruch)

Daher ist die Annahme unmöglich: r6c9 kann nicht 3 sein und der Kandidat 3 kann eliminiert werden.

Beispiele

Diese Bilder zeigen weitere leere Rechteckmuster. Verwenden Sie sie als Referenzen für „Boxkreuz/L-Form + kurze Kette + Eliminierung (rot)“:

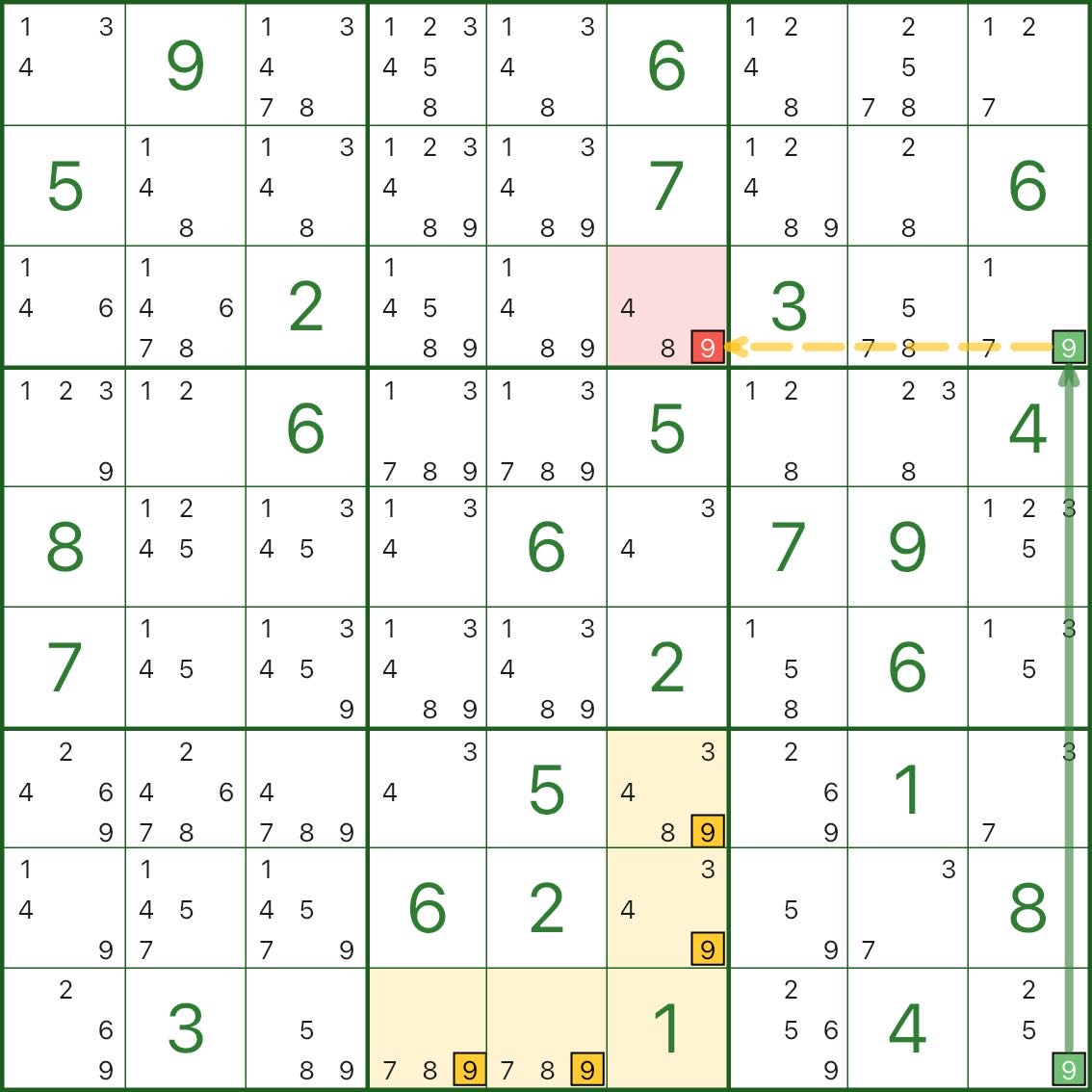
Empty Rectangle example A

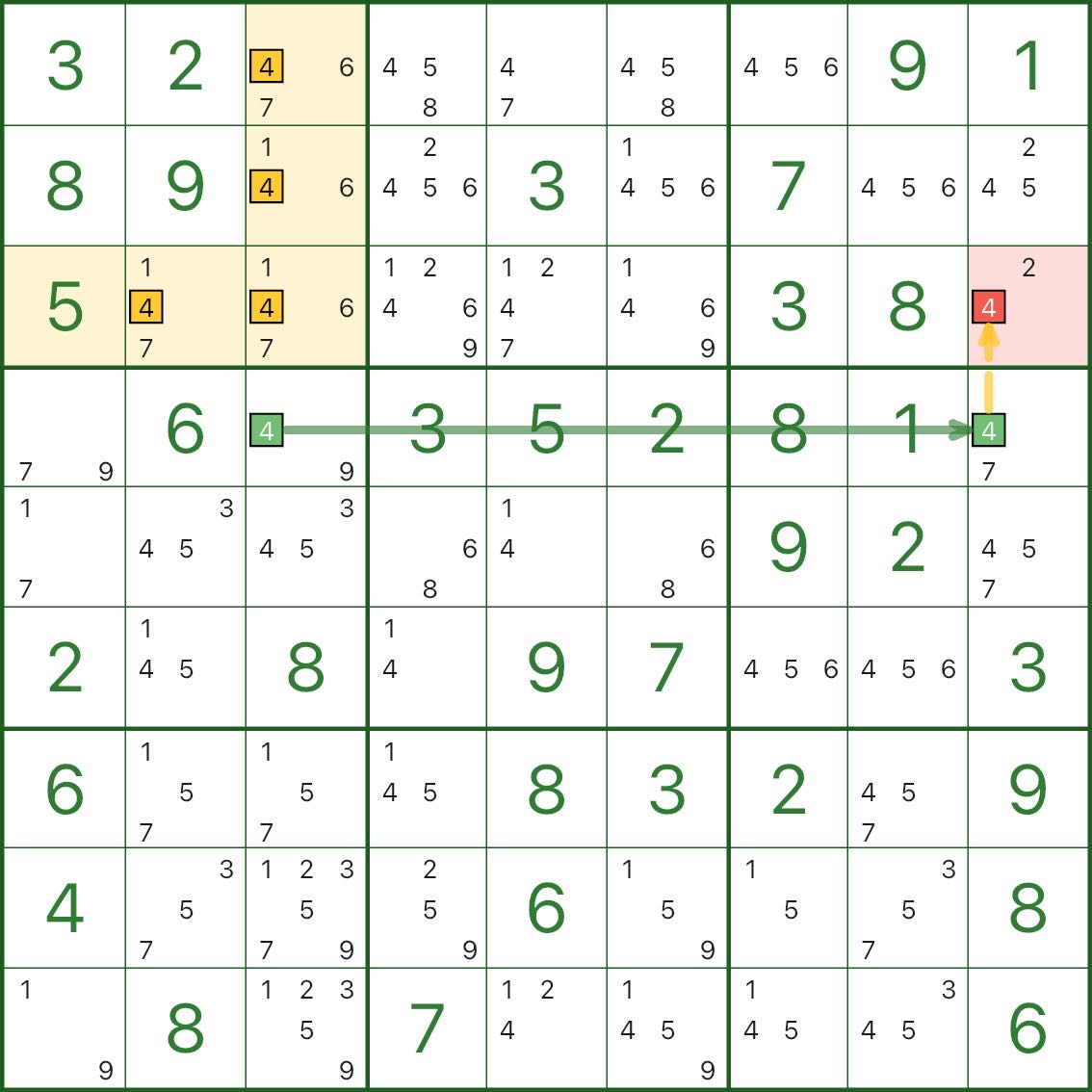
Empty Rectangle example B

So finden Sie ein leeres Rechteck

Einzeilige Checkliste: Suchen Sie ein Kästchen, in dem d Kandidaten eine Kreuz-/L-Form bilden, verwenden Sie dann eine kurze Kette, die dazu führen würde, dass dem Kästchen die Plätze für d ausgehen, und eliminieren Sie den roten Kandidaten durch Widerspruch.

In einem echten Puzzle:

Wählen Sie eine Ziffer d
Überprüfen Sie in einem Kästchen, ob alle d Kandidaten auf einer Zeile + einer Spalte liegen (Kreuz-/L-Form)
Suchen Sie nach einer kurzen Kette, sodass die Annahme, dass ein roter Kandidat wahr ist, d auf diese Linien zwingt
Wenn diese Annahme dazu führt, dass das Kästchen keinen Platz für d enthält, eliminiere den roten Kandidaten d