Grundfärbung

Voraussetzung: Chain Basics

Beschreibung

Die Grundfärbung ist eine Technik zur Kandidateneliminierung einzelner Ziffern: Konzentrieren Sie sich auf eine Ziffer d und verwenden Sie nur starke Links aus Bilokationen (eine Zeile/Spalte/ein Feld, in der die Ziffer d in genau zwei Kandidatenzellen vorkommt).

Sie „färben“ die Kandidaten entlang starker Links mit zwei Farben (blau/gelb).
Diese beiden Farben stellen zwei sich gegenseitig ausschließende Ableitungswege dar: Bei einer starken Verbindung ist genau ein Ende wahr, daher wechselt die Farbe.

In einer Farbkette kann man sich Blau/Gelb als zwei gegensätzliche Annahmen vorstellen:

• Angenommen, Blau ist wahr ⇒ Gelb ist falsch
• Angenommen, Blau ist falsch ⇒ Gelb ist wahr

Im selben starken Link muss also eine der beiden Farben wahr sein.

Die Grundfärbung führt normalerweise zu zwei Arten von Schlussfolgerungen:

1. Falle: Ein roter Kandidat kann einen blauen und einen gelben Kandidaten sehen → der rote Kandidat kann eliminiert werden
2. Widerspruch gleicher Farbe: Zwei Kandidaten derselben Farbe erscheinen in einem Haus → die gesamte Farbe ist unmöglich und kann eliminiert werden

---

Falle

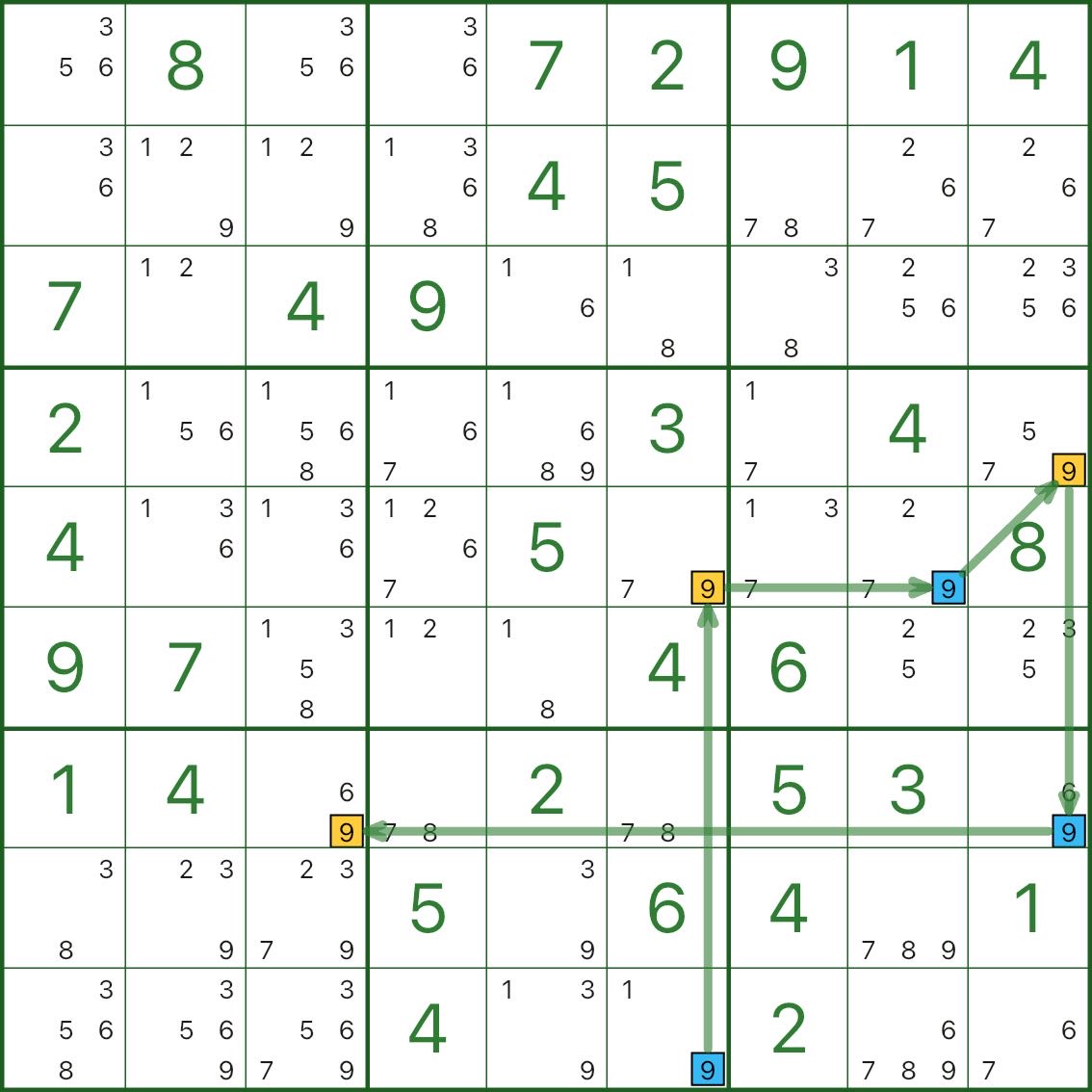
In Bild 1 ist die Zielziffer 9. Wir färben eine starke Gliederkette beginnend mit r9c6; der andere Endpunkt ist r7c3 (blau/gelb).

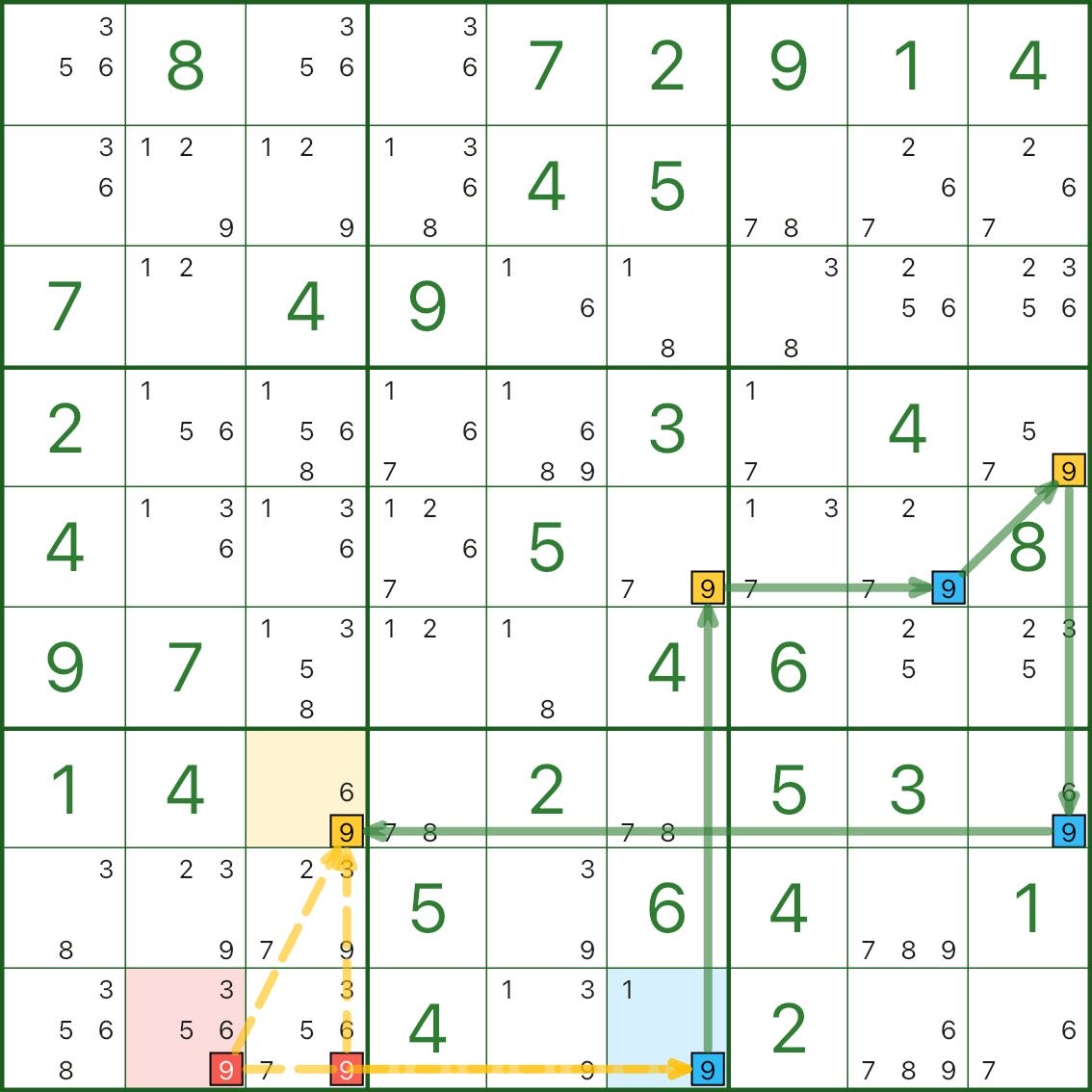
In Bild 2 sind die roten Kandidaten Kandidat 9 in r9c2 und Kandidat 9 in r9c3.
Warum können wir sie entfernen? Der Schlüsselgedanke ist:

• Wenn blau wahr ist, ist der blaue Endpunkt (z. B. r9c6) 9. Da die roten Kandidaten ihn sehen können, stehen sie im Konflikt mit dem blauen Endpunkt und können nicht 9 sein.
• Wenn blau falsch ist, muss der gelbe Endpunkt auf demselben starken Link wahr sein (z. B. ist r7c3 9). Die roten Kandidaten können es auch sehen, also stehen sie immer noch im Konflikt und können nicht 9 sein.

So oder so dürfen die roten Kandidaten nicht 9 sein und können daher eliminiert werden.

---

Gleichfarbiger Widerspruch

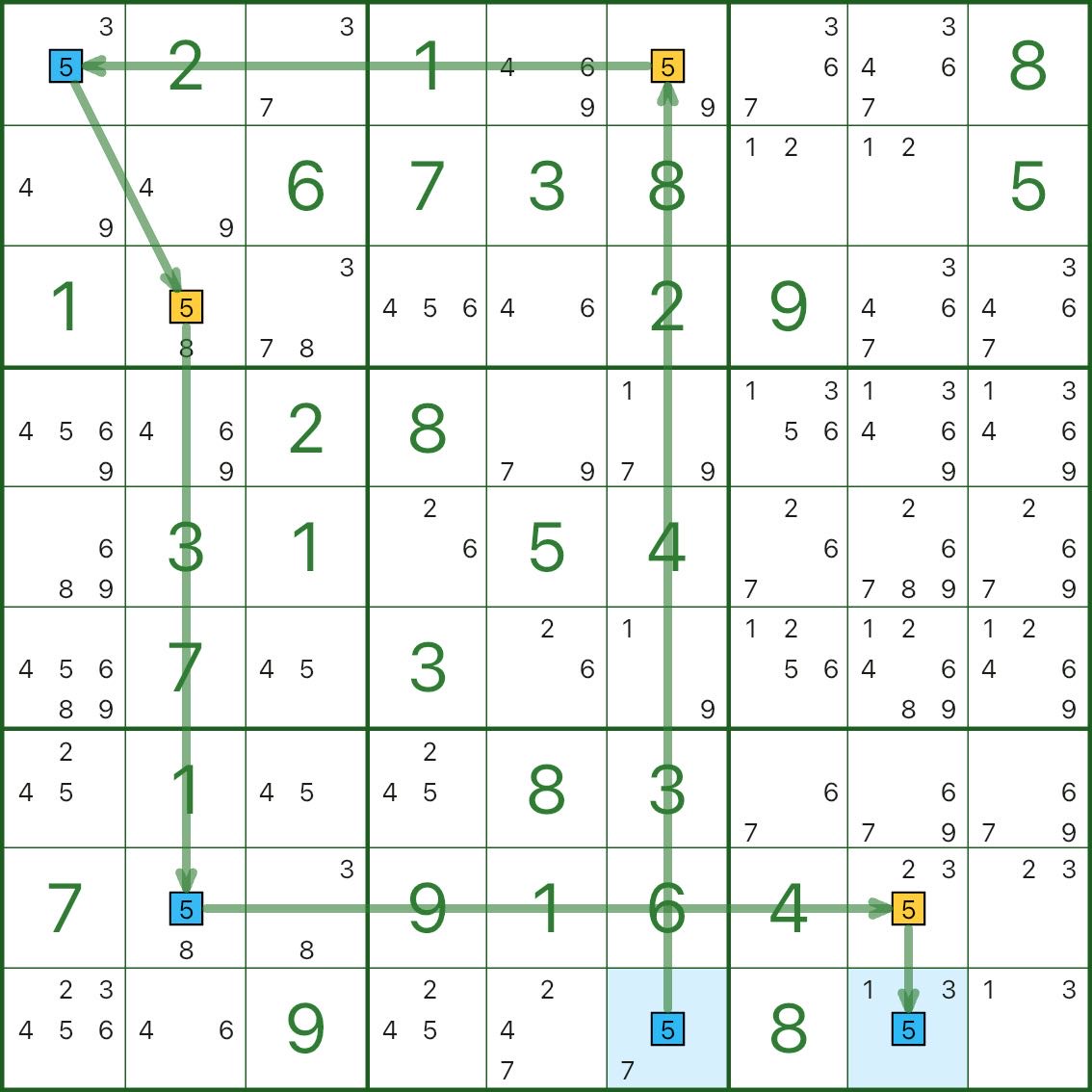
In Bild 3 ist die Zielziffer 5. Beginnend mit r9c6 zwingt die Kette schließlich r9c8 dazu, ebenfalls eine blaue 5 zu sein.
Aber r9c6 und r9c8 befinden sich in derselben Zeile, daher können sie nicht beide 5 sein – das ist ein gleichfarbiger Widerspruch.

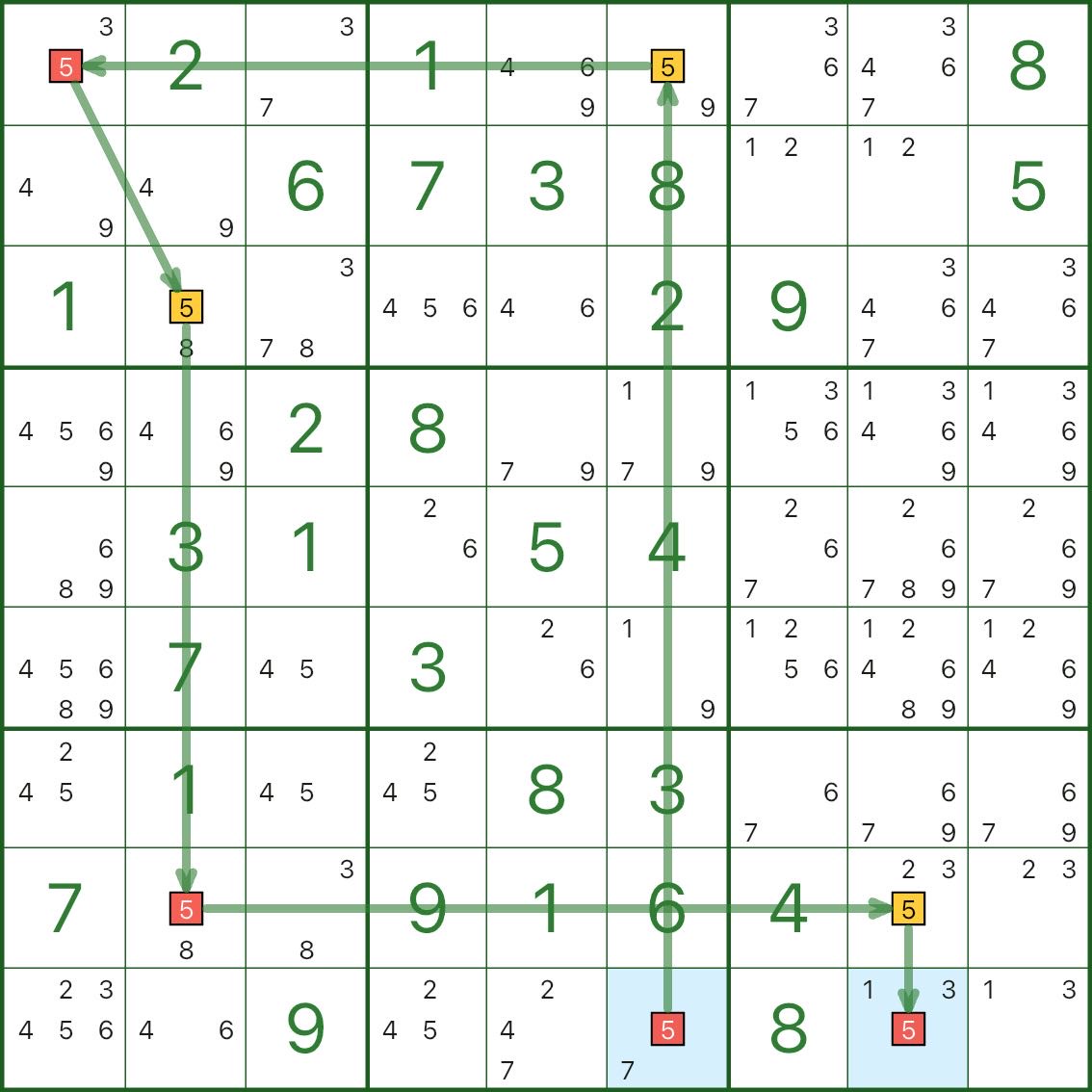
Daher ist die blaue Route unmöglich:
Alle blauen 5er-Kandidaten können eliminiert werden (dargestellt in Bild 4).

---

So finden Sie grundlegende Farben

Einzeilige Checkliste: Finden Sie starke Links zur Bilokation, färben Sie sie blau/gelb und suchen Sie dann nach Fallen oder gleichfarbigen Widersprüchen.

In einem echten Puzzle:

1. Wählen Sie eine Ziffer d
2. Finden Sie starke Bilokationsverbindungen für d (eine Einheit mit genau 2 Kandidaten von d)
3. Beginnen Sie an einer beliebigen Stelle und wechseln Sie die Farben entlang starker Verbindungen
4. Suchen Sie nach:
   • ein roter Kandidat, der einen blauen und einen gelben sieht → Falleneliminierung
   • zwei gleichfarbige Kandidaten in einer Einheit → die gesamte Farbe eliminieren