Kettengrundlagen

Starke Links / schwache Links / Alternation (AIC)

Ketten sind ein zentraler Baustein für viele fortgeschrittene Sudoku-Techniken.
Im Grunde ist eine Kette nur eine Folge von „Wenn…dann…“-Implikationen, die es ermöglichen, Schlussfolgerungen über das Raster zu ziehen.

Nach diesem Kapitel werden sich fortgeschrittene Hinweise wie einstellige Ketten, Drachen, Wolkenkratzer, Medusa und AIC viel besser lesbar anfühlen.

Wir verwenden r1c1, um auf eine Zellenposition zu verweisen:
r = Zeile, c = Spalte.

Um die Diagramme leichter verständlich zu machen, verwenden wir:

• Grüne durchgezogene Linie: starke Verbindung
• Gelbe gestrichelte Linie: schwaches Glied
• Blauer/gelber Kandidatenhintergrund: zwei sich gegenseitig ausschließende „Zustände“, um den Wechsel zu visualisieren
• Roter Kandidat: der Kandidat, der in diesem Schritt eliminiert werden soll

Zur Erinnerung: Eine Kette ist bidirektional. Pfeile dienen lediglich der besseren Lesbarkeit.

---

Was ist eine Kette?

Kurz gesagt, eine Kette verbindet Kandidatenbeziehungen, sodass Sie weiterhin die „Wenn…dann…“-Logik anwenden können:

Wenn A nicht möglich ist, muss B wahr sein;
wenn B wahr ist, dann muss C falsch sein;
…

Eine Kette besteht aus:

• Knoten: Kandidaten (ein Ziffernkandidat in einer Zelle)
• Links: Beziehungen zwischen Kandidaten (stark / schwach)

Eine Kette bedeutet nicht unbedingt „Wir löschen immer den Anfang“. Es ist eher ein Argumentationspfad:

• Erreichen Sie einen Widerspruch ⇒ beweisen Sie, dass ein Kandidat nicht wahr sein kann → beseitigen Sie ihn
• Erreichen Sie eine erzwungene Wahrheit ⇒ beweisen Sie, dass ein Kandidat wahr sein muss → legen Sie einen Wert fest

Dieser Artikel konzentriert sich auf die häufigsten „einstelligen Ketten“: Überlegungen zu Kandidaten mit einer Ziffer d.
(Zweiwertige Zellbeziehungen und starke Gruppen-/Regionsverknüpfungen werden später behandelt.)

---

Starke Links und schwache Links

Starke Verbindung (konjugiertes Paar)

Mnemonik: entweder-oder.

Wenn in derselben Einheit (Zeile/Spalte/Box) eine Ziffer d in genau zwei Kandidatenzellen vorkommt, bilden diese beiden Kandidaten eine starke Verbindung (ein konjugiertes Paar).

Die wichtigste Implikation ist „NICHT erzwingt JA“:

• Wenn NICHT A, dann B (Wenn A nicht d ist, dann muss B d sein)
• Wenn NICHT B, dann A

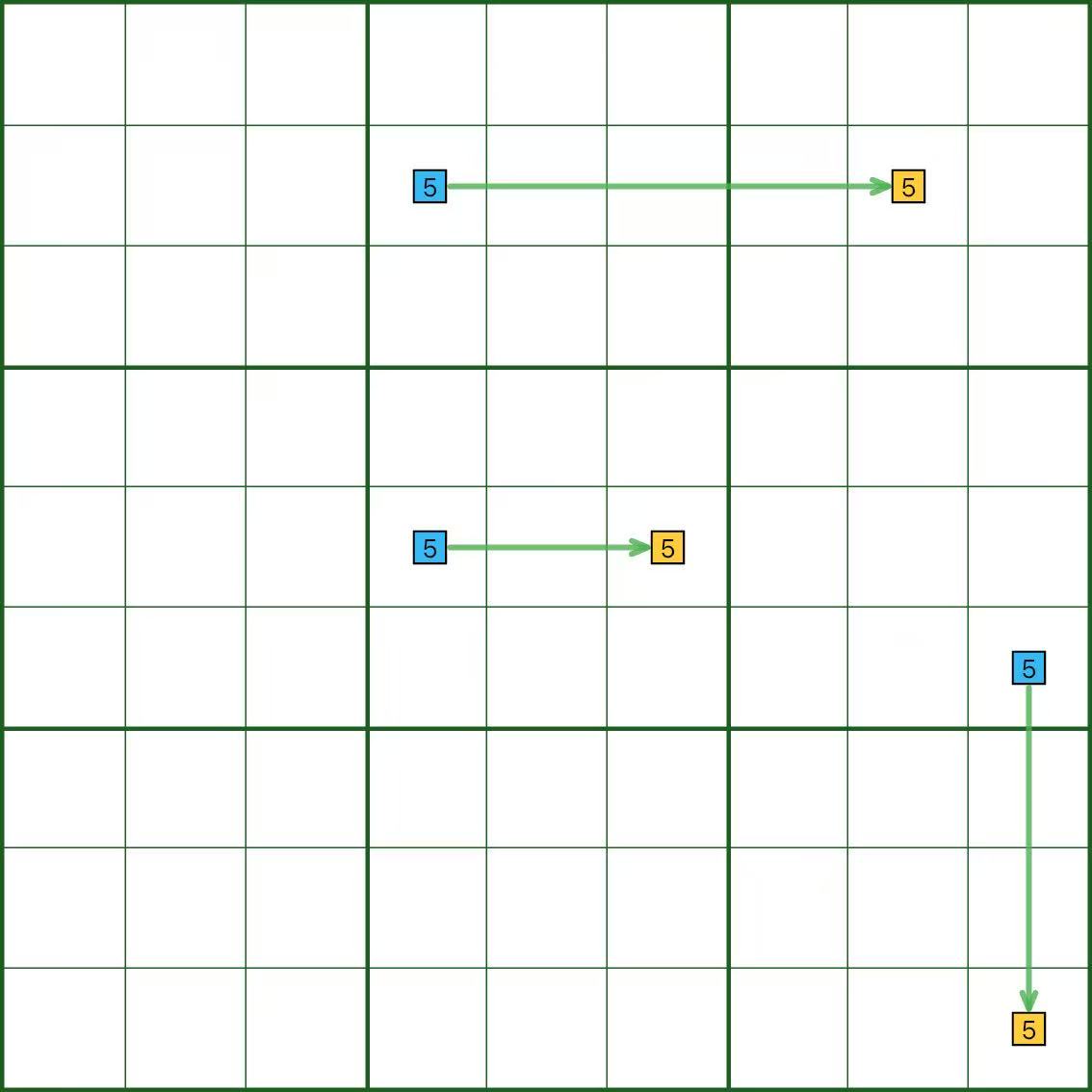
Im Diagramm bildet Ziffer 5 starke Verknüpfungen in einer Zeile, einer Spalte und einem Kästchen.
Sie können es von beiden Seiten lesen; Pfeile sind lediglich eine Lesehilfe.

Wichtiger Hinweis: Jeder starke Link ist auch ein schwacher Link.
Da die beiden Kandidaten dieselbe Einheit haben, können sie nicht beide wahr sein:

• Wenn A, dann NICHT B (Wenn A d ist, dann ist B nicht d)

Zusammenfassung in einer Zeile:

Starke Verbindung = schwache Exklusivität + „Eines davon muss wahr sein“

Schwaches Glied

Merksatz: Wenn ihr euch seht, könnt ihr nicht beide wahr sein.

Ein schwaches Glied drückt eines aus:

Zwei Kandidaten können nicht beide wahr sein.

In einstelligen Ketten besteht das häufigste schwache Glied aus zwei Kandidaten derselben Ziffer d in derselben Einheit.

Implikation:

• Wenn A, dann NICHT B

Aber nicht umgekehrt:

• Wenn A falsch ist, können Sie nicht auf B schließen (es kann eine dritte Stelle geben).

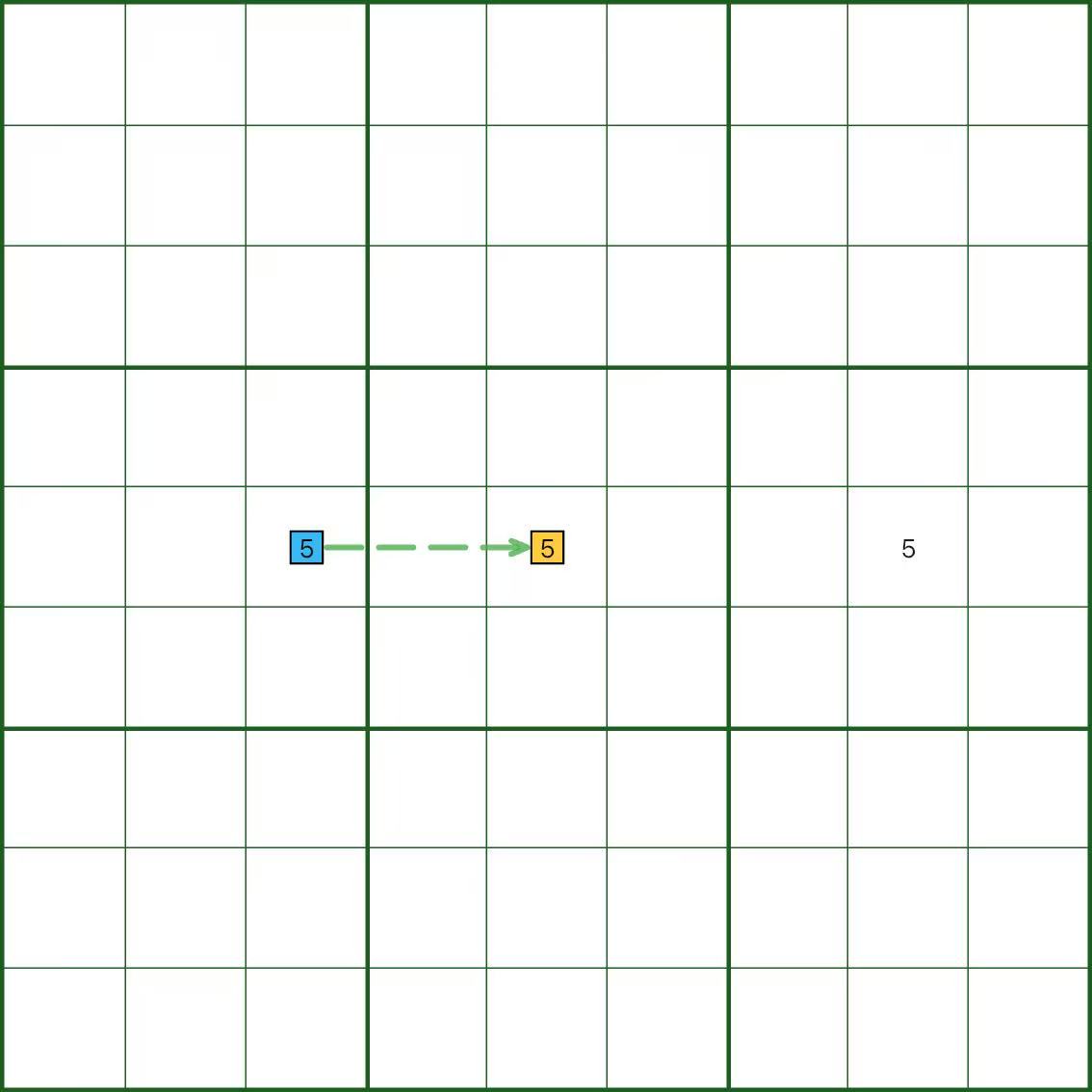
Im Diagramm enthält Ziffer 5 drei Kandidatenzellen in einer Reihe, sodass jedes Paar schwach verknüpft ist.
Das Bild zeigt nur ein gestricheltes Segment, um zu zeigen, wie ein schwaches Glied aussieht.

---

Wie funktionieren Ketten?

Beachten Sie für die Ausbreitung entlang einer Kette zwei Regeln:

1. Wahr → (schwach) → Falsch
   Schwache Links sind exklusiv: Wenn A wahr ist, muss B falsch sein.
2. Falsch → (stark) → Wahr
   Starke Verknüpfungen sind Entweder-Oder: Wenn A falsch ist, muss der andere Kandidat wahr sein.

Eine Arbeitskette wechselt also typischerweise ab:

Falsch – (stark) → Wahr – (schwach) → Falsch – (stark) → Wahr – (schwach) → Falsch …

Warum abwechseln?

• Schwach-Schwach-Brüche: „falsch“ breitet sich nicht über einen schwachen Link aus
• Stark-Stark kann eine Verbindung herstellen, aber in vielen Rätseln entspricht es oft einfacheren Mustern, sodass Ketten für die alternierende Ausbreitung am nützlichsten sind

---

Beispiel

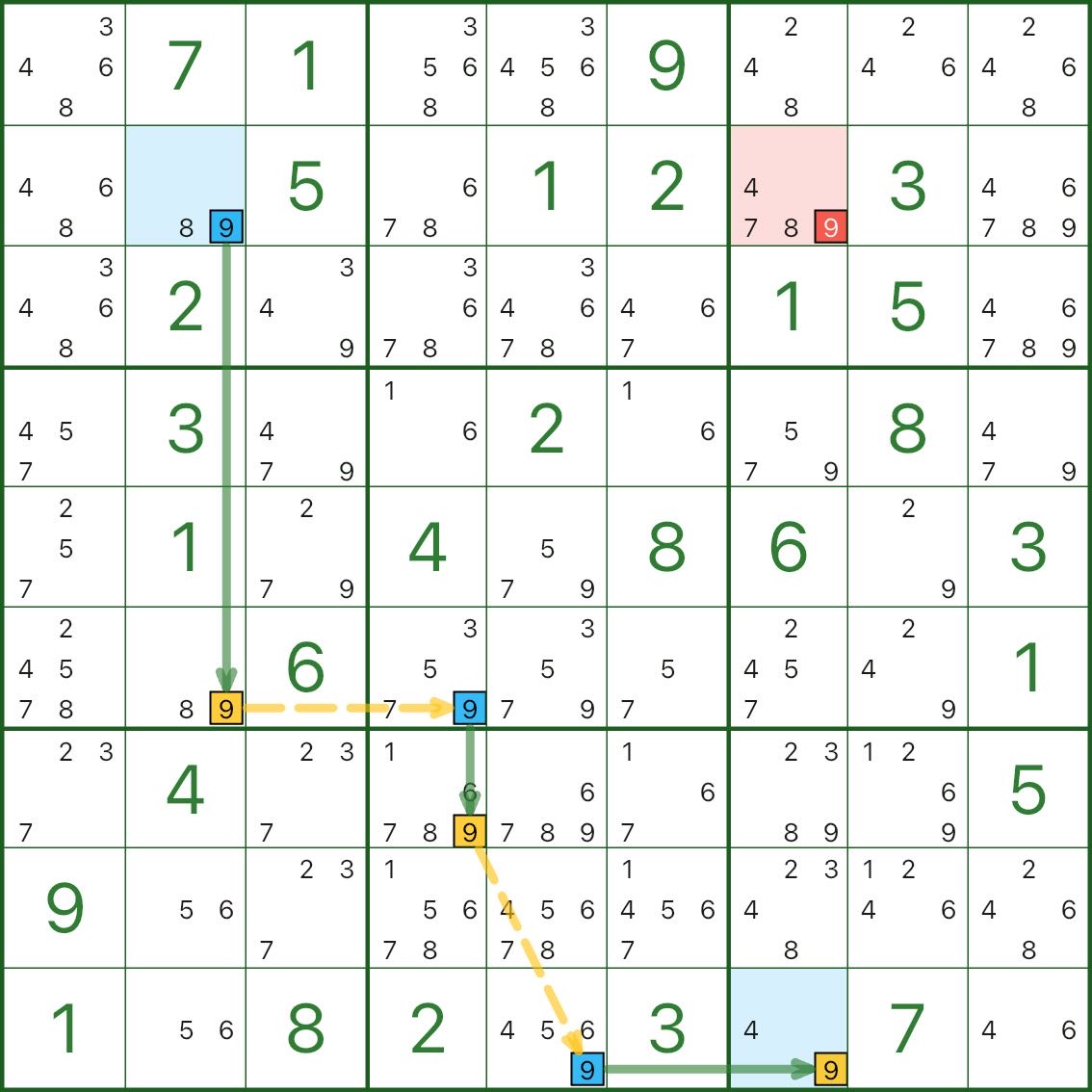
Im Diagramm ist der rote Kandidat Ziffer 9 in r2c7.

Lesen Sie es so:

1. Ab dem markierten Anfang: Sobald r2c2 NICHT 9 ist, breitet sich die Kette aus, um r9c7 = 9 zu erzwingen
   (Sie können den sauberen Wechsel sehen Falsch → Wahr → Falsch → Wahr → Falsch → Wahr)

2. Verwenden Sie nun einen Widerspruch: Nehmen Sie an, der rote Kandidat r2c7 = 9 ist wahr

   • r2c7 sieht r2c2 in derselben Zeile, daher kann r2c2 nicht 9 sein (r2c2(9) ist falsch)
   • Verbreiten Sie dieses „falsch“ durch die Kette und erzwingen Sie, dass r9c7(9) wahr ist
   • r2c7 und r9c7 befinden sich in derselben Spalte, daher können sie nicht beide 9 sein → Widerspruch

Daher kann r2c7 nicht 9 sein und dieser rote Kandidat kann eliminiert werden.

---

Üben

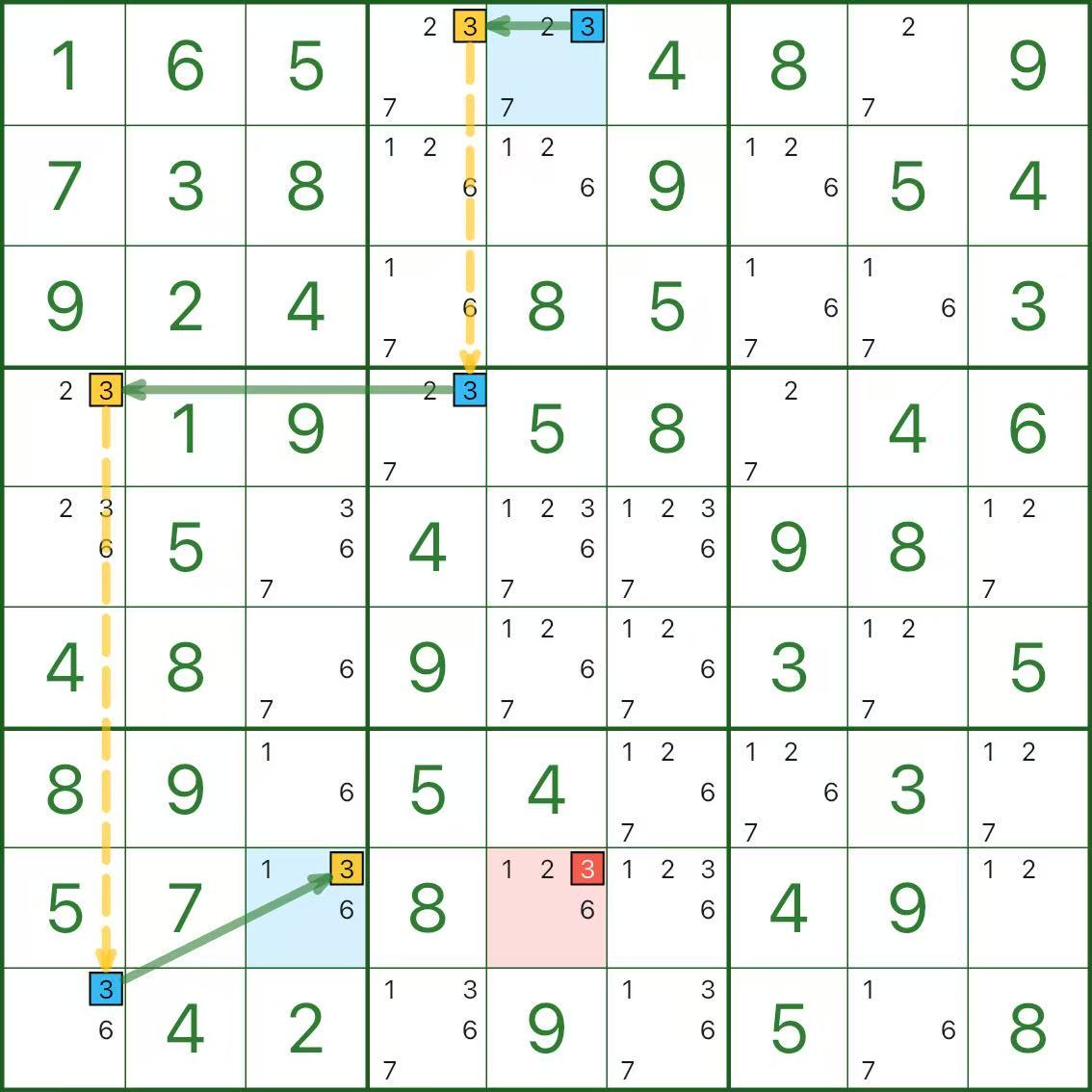
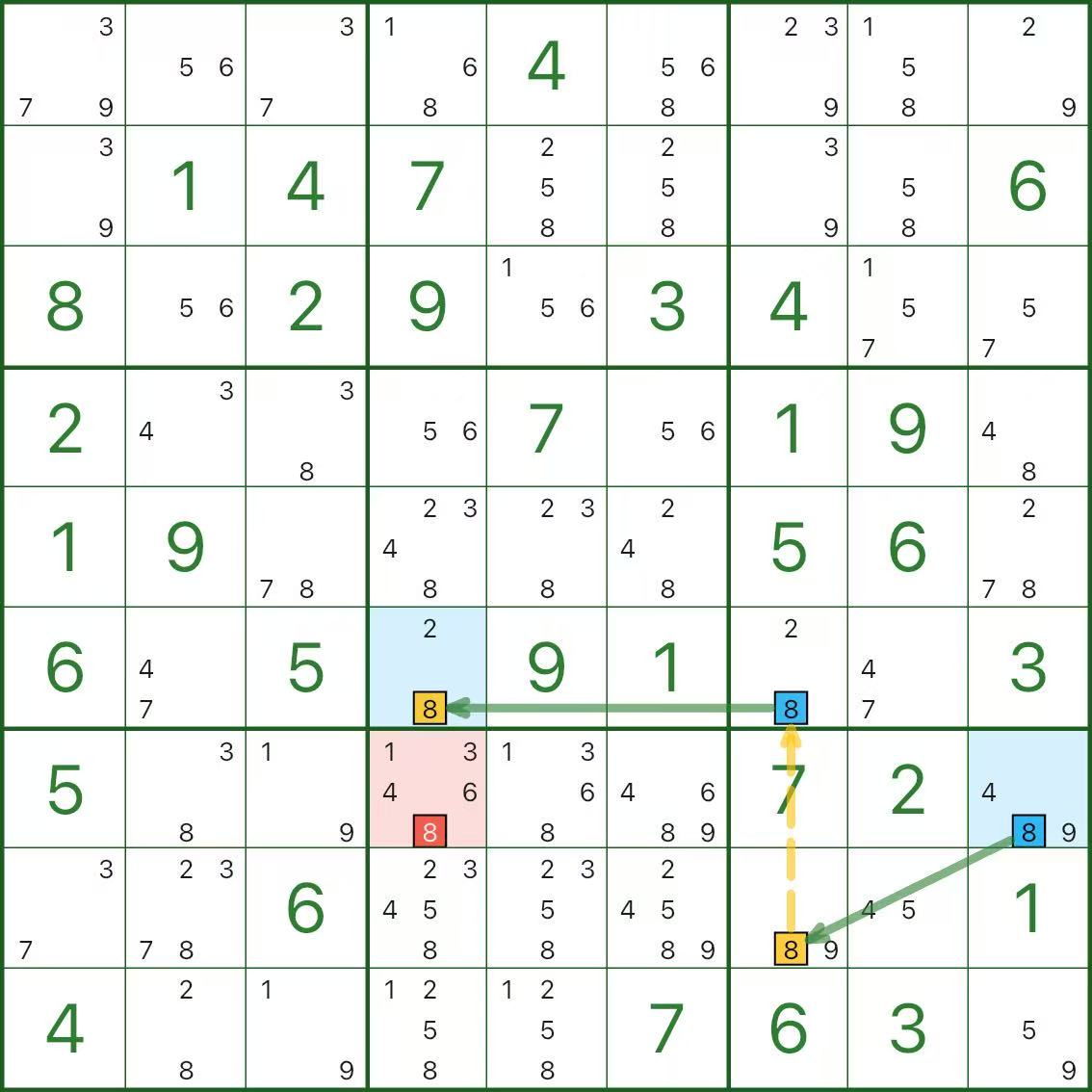
Die folgenden drei Diagramme sind alle einstellige Ketten. Nehmen Sie sich Zeit.

Drei kurze Fragen zur Selbstkontrolle:

1. Welche Segmente sind starke Links und warum sind sie „entweder-oder“?
2. Welche Segmente sind schwache Glieder und warum schließen sie sich gegenseitig aus?
3. Warum führt der rote Kandidat zu einem Widerspruch?

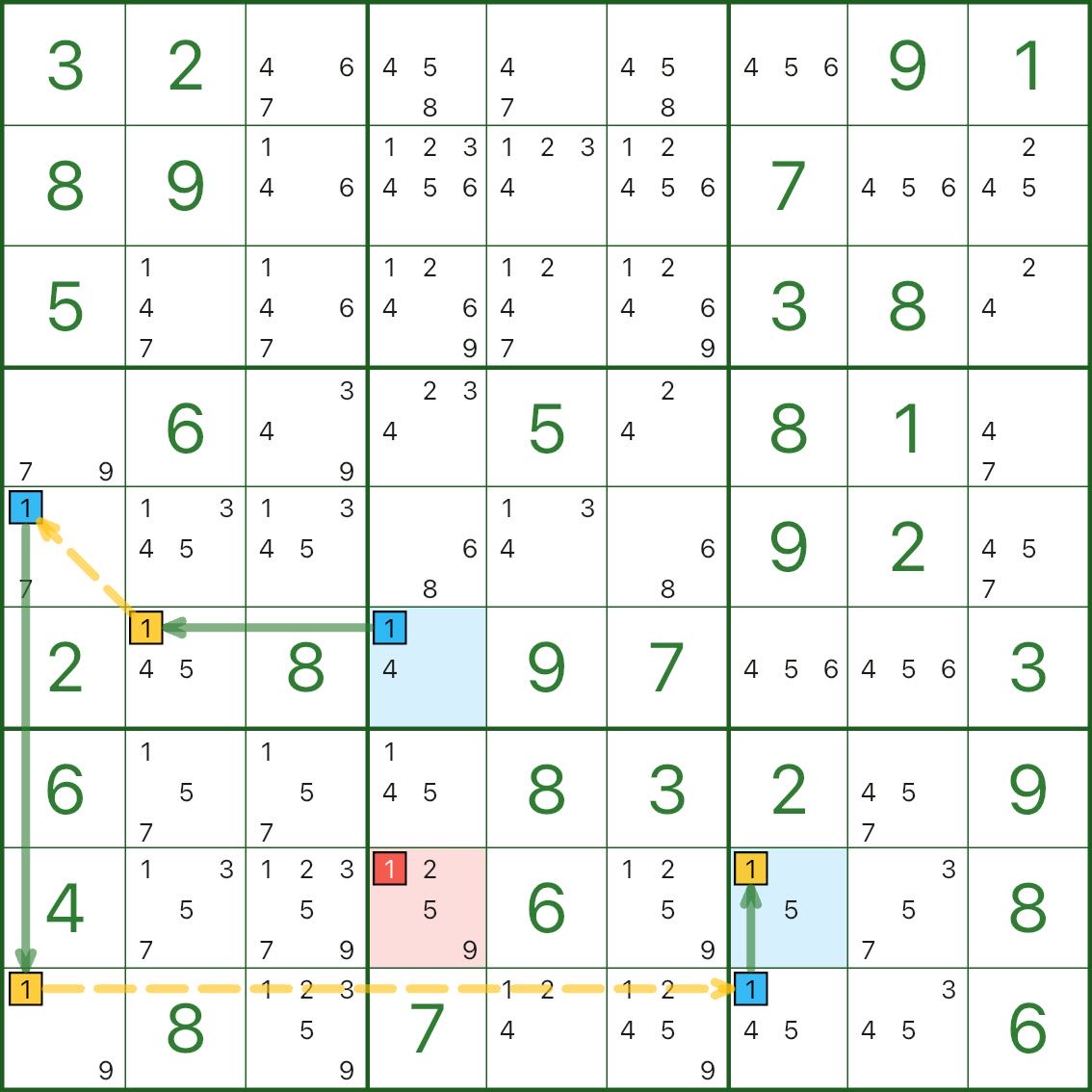
Wenn es sich anfangs etwas verdreht anfühlt, ist das völlig normal.
Das ist eine Kette: die Grundlage vieler fortgeschrittener Techniken – machen Sie sich damit vertraut, bevor Sie fortfahren.